Funkcijske nule. Nula funkcije Kako odrediti nule funkcije
Funkcija jedan je od najvažnijih matematičkih pojmova. Ovisnost funkcije - varijable na iz varijable x, ako je svaka vrijednost x odgovara jednoj vrijednosti na. Varijabilna x naziva nezavisna varijabla ili argument. Varijabilna na naziva zavisna varijabla. Sve vrijednosti nezavisne varijable (varijable x) čine domenu definicije funkcije. Sve vrijednosti koje zavisna varijabla poprima (varijabla g), čine raspon vrijednosti funkcije.
Grafikon funkcije nazivamo skup svih točaka koordinatne ravnine čije su apscise jednake vrijednostima argumenta, a ordinate jednake odgovarajućim vrijednostima funkcije, odnosno vrijednostima varijable se crtaju duž apscisne osi x, a vrijednosti varijable su iscrtane duž ordinatne osi g. Da biste nacrtali graf funkcije, morate znati svojstva funkcije. O glavnim svojstvima funkcije bit će riječi u nastavku!
Za izradu grafa funkcije preporučujemo korištenje našeg programa - Izrada grafa funkcija na mreži. Ako imate bilo kakvih pitanja tijekom proučavanja materijala na ovoj stranici, uvijek ih možete postaviti na našem forumu. Također na forumu će vam pomoći riješiti probleme iz matematike, kemije, geometrije, teorije vjerojatnosti i mnogih drugih predmeta!
Osnovna svojstva funkcija.
1) Domena funkcije i područje funkcije.
Domena funkcije je skup svih valjanih valjanih vrijednosti argumenata x(varijabilno x), za koju je funkcija y = f(x) odlučan.
Raspon funkcije je skup svih realnih vrijednosti g, što funkcija prihvaća.
U elementarnoj matematici funkcije se proučavaju samo na skupu realnih brojeva.
2) Funkcijske nule.
Funkcija nula je vrijednost argumenta pri kojoj je vrijednost funkcije jednaka nuli.
3) Intervali konstantnog predznaka funkcije.
Intervali konstantnog predznaka funkcije su skupovi vrijednosti argumenata na kojima su vrijednosti funkcije samo pozitivne ili samo negativne.
4) Monotonost funkcije.
Rastuća funkcija (u određenom intervalu) je funkcija kod koje većoj vrijednosti argumenta iz tog intervala odgovara veća vrijednost funkcije.
Opadajuća funkcija (u određenom intervalu) je funkcija kod koje manja vrijednost funkcije odgovara većoj vrijednosti argumenta iz tog intervala.
5) Parna (neparna) funkcija.
Parna funkcija je funkcija čija je definicijska domena simetrična s obzirom na ishodište i za bilo koji x iz domene definicije jednakost f(-x) = f(x). Graf parne funkcije je simetričan u odnosu na ordinatu.
Neparna funkcija je funkcija čija je definicijska domena simetrična s obzirom na ishodište i za bilo koji x iz domene definicije jednakost je istinita f(-x) = - f(x). Graf neparne funkcije je simetričan u odnosu na ishodište.
6) Ograničene i neograničene funkcije.
Funkcija se naziva ograničenom ako postoji pozitivan broj M takav da je |f(x)| ≤ M za sve vrijednosti x. Ako takav broj ne postoji, funkcija je neograničena.
7) Periodičnost funkcije.
Funkcija f(x) je periodična ako postoji broj T različit od nule takav da je za bilo koji x f(x+T) = f(x). Taj najmanji broj naziva se periodom funkcije. Sve trigonometrijske funkcije su periodične. (Trigonometrijske formule).
Nakon što ste proučili ova svojstva funkcije, možete jednostavno istražiti funkciju i, koristeći svojstva funkcije, možete izgraditi graf funkcije. Također pogledajte gradivo o tablici istinitosti, tablici množenja, periodnom sustavu, tablici izvodnica i tablici integrala.
Funkcijske nule
Što su funkcijske nule? Kako analitički i grafički odrediti nulte točke funkcije?
Funkcijske nule- ovo su vrijednosti argumenata pri kojima je funkcija jednaka nuli.
Da biste pronašli nulte točke funkcije zadane formulom y=f(x), trebate riješiti jednadžbu f(x)=0.
Ako jednadžba nema korijena, funkcija nema nula.
1) Nađite nulte točke linearne funkcije y=3x+15.
Da biste pronašli nulte točke funkcije, riješite jednadžbu 3x+15 =0.
Dakle, nula funkcije je y=3x+15 - x= -5.
2) Pronađite nulte točke kvadratne funkcije f(x)=x²-7x+12.
Da biste pronašli nulte točke funkcije, riješite kvadratnu jednadžbu
Njeni korijeni x1=3 i x2=4 su nule ove funkcije.
3) Pronađite nulte točke funkcije
Razlomak ima smisla ako je nazivnik različit od nule. Prema tome, x²-1≠0, x² ≠ 1, x ≠±1. To jest, domena definicije date funkcije (DO)
Od korijena jednadžbe x²+5x+4=0 x1=-1 x2=-4 samo je x=-4 uključeno u domenu definicije.
Da biste pronašli nulte točke funkcije prikazane grafički, morate pronaći točke presjeka grafa funkcije s osi apscisa.
Ako graf ne siječe Ox-os, funkcija nema nula.
funkcija čiji je graf prikazan na slici ima četiri nule -
U algebri se problem pronalaženja nula funkcija javlja i kao samostalan zadatak i pri rješavanju drugih problema, na primjer, pri proučavanju funkcije, rješavanju nejednakosti itd.
www.algebraclass.ru
Pravilo nula funkcija
Osnovni pojmovi i svojstva funkcija
Pravilo (zakon) dopisivanja. Monotona funkcija .
Ograničene i neograničene funkcije. Kontinuirano i
diskontinuirane funkcije . Parne i neparne funkcije.
Periodična funkcija. Razdoblje funkcije.
Funkcijske nule . Asimptota .
Područje definiranja i područje vrijednosti funkcije. U elementarnoj matematici funkcije se proučavaju samo na skupu realnih brojeva R . To znači da argument funkcije može uzeti samo one stvarne vrijednosti za koje je funkcija definirana, tj. također prihvaća samo stvarne vrijednosti. Gomila x sve važeće valjane vrijednosti argumenata x, za koju je funkcija g = f (x) je definiran, tzv domena funkcije. Gomila Y sve prave vrijednosti g, koje funkcija prihvaća, naziva se raspon funkcija. Sada možemo dati precizniju definiciju funkcije: Pravilo (zakon) korespondencije između skupova x I Y , prema kojem za svaki element iz skupa x možete pronaći jedan i samo jedan element iz skupa Y, naziva se funkcija .
Iz ove definicije slijedi da se funkcija smatra definiranom ako:
— navedena je domena definicije funkcije x ;
— naveden je raspon funkcija Y ;
— poznato je pravilo (zakon) dopisivanja, i to takovo, da za svaki
vrijednost argumenta, može se pronaći samo jedna vrijednost funkcije.
Ovaj zahtjev jedinstvenosti funkcije je obavezan.
Monotona funkcija.
Ako za bilo koje dvije vrijednosti argumenta x 1 i x 2. uvjeta x 2 > x 1 slijedi f (x 2) > f (x 1), zatim funkcija f (x) Zove se povećavajući se; ako za bilo koji x 1 i x 2. uvjeta x 2 > x 1 slijedi f (x 2)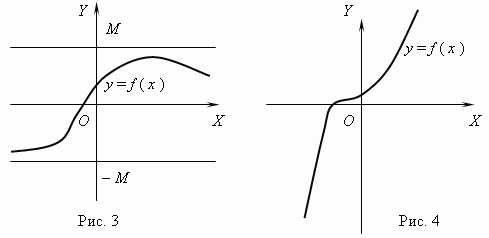 
Funkcija prikazana na slici 3 je ograničena, ali nije monotona. Funkcija na slici 4 je upravo suprotna, monotona, ali neograničena. (Molim vas, objasnite ovo!).
Kontinuirane i diskontinuirane funkcije. Funkcija g = f (x) Zove se stalan u točki x = a, ako:
1) funkcija je definirana kada x = a, tj. f (a) postoji;
2) postoji konačan limit lim f (x) ;
Ako barem jedan od ovih uvjeta nije ispunjen, tada se funkcija poziva Eksplozivno u točki x = a .
Ako je funkcija kontinuirana tijekom svatko točke svoje domene definicije, onda se zove kontinuirana funkcija.
Parne i neparne funkcije. Ako za bilo koji x iz domene definicije funkcije vrijedi: f (— x) = f (x), tada se funkcija poziva čak; ako se dogodi: f (— x) = — f (x), tada se funkcija poziva neparan. Graf parne funkcije simetričan u odnosu na Y os(slika 5), graf neparne funkcije Sim metrika s obzirom na ishodište(slika 6).
Periodična funkcija. Funkcija f (x) — periodički, ako takvo što postoji različit od nule broj T za što bilo koji x iz domene definicije funkcije vrijedi: f (x + T) = f (x). Ovaj najmanje broj se zove razdoblje funkcije. Sve trigonometrijske funkcije su periodične.
Primjer 1. Dokažite taj grijeh x ima razdoblje od 2.
Rješenje: Znamo da je grijeh ( x+ 2 n) = grijeh x, Gdje n= 0, ± 1, ± 2, …
Dakle, dodatak 2 n ne na argument sinusa
mijenja svoju vrijednost e. Postoji li još jedan broj uz ovo
Hajdemo to pretvarati P– takav broj, tj. jednakost:
vrijedi za bilo koju vrijednost x. Ali onda jest
mjesto i na x= / 2, tj.
grijeh(/2 + P) = grijeh / 2 = 1.
Ali prema redukcijskoj formuli sin (/ 2 + P) = cos P. Zatim
iz zadnje dvije jednakosti slijedi da je cos P= 1, ali mi
znamo da je to istina samo kad P = 2 n. Od najmanjeg
broj različit od nule od 2 n je 2, onda ovaj broj
i postoji period grijeh x. Na sličan način može se dokazati da je 2
također je razdoblje za cos x .
Dokažite da su funkcije tan x i krevetić x imati mjesečnicu .
Primjer 2. Koji broj je period funkcije sin 2 x ?
Rješenje: Razmotrite grijeh 2 x= grijeh (2 x+ 2 n) = sin [ 2 ( x + n) ] .
Vidimo da se dodaje n na argument x, ne mijenja se
vrijednost funkcije. Najmanji broj različit od nule
iz n je , dakle ovo je period sin 2 x .
Funkcijske nule. Poziva se vrijednost argumenta pri kojoj je funkcija jednaka 0 nula ( root) funkcija. Funkcija može imati više nula. Na primjer, funkcija g = x (x + 1) (x- 3) ima tri nule: x = 0, x = — 1, x= 3. Geometrijski nulta funkcija – ovo je apscisa točke presjeka grafa funkcije s osi x .
Slika 7 prikazuje graf funkcije s nulama: x = a , x = b I x = c .
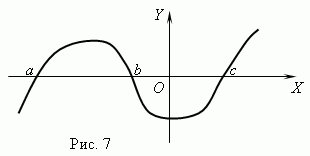
Asimptota. Ako se graf funkcije neograničeno približava određenom pravcu dok se udaljava od ishodišta, tada se taj pravac naziva asimptota.
Tema 6. “Metoda intervala.”
Ako je f (x) f (x 0) za x x 0, tada se poziva funkcija f (x). kontinuirana u točki x 0.
Ako je funkcija kontinuirana u svakoj točki nekog intervala I, tada se zove kontinuirano na intervalu I (interval I naziva se interval kontinuiteta funkcije). Graf funkcije na tom intervalu je neprekinuta crta, za koju kažu da se može "nacrtati bez podizanja olovke s papira".
Svojstvo neprekidnih funkcija.
Ako je na intervalu (a ; b) funkcija f neprekidna i ne nestaje, tada ona na tom intervalu zadržava konstantan predznak.
Na ovom se svojstvu temelji metoda rješavanja nejednadžbi s jednom varijablom, metoda intervala. Neka je funkcija f(x) neprekidna na intervalu I i nestaje u konačnom broju točaka u tom intervalu. Po svojstvu kontinuiranih funkcija te točke dijele I na intervale u kojima kontinuirana funkcija f(x) c zadržava konstantan predznak. Za određivanje tog predznaka dovoljno je izračunati vrijednost funkcije f(x) u bilo kojoj točki iz svakog takvog intervala. Na temelju toga dobivamo sljedeći algoritam za rješavanje nejednadžbi metodom intervala.
Intervalna metoda za nejednakosti oblika
Metoda intervala. Prosječna razina.
Želite li testirati svoju snagu i saznati rezultat koliko ste spremni za Jedinstveni državni ispit ili Jedinstveni državni ispit?
Linearna funkcija
Funkcija oblika naziva se linearna. Uzmimo funkciju kao primjer. Pozitivan je na 3″>, a negativan na. Točka je nula funkcije (). Pokažimo predznake ove funkcije na brojevnoj osi:
Kažemo da “funkcija mijenja predznak prolaskom kroz točku”.
Vidljivo je da predznaci funkcije odgovaraju položaju grafa funkcije: ako je graf iznad osi, znak je “ ”, ako je ispod nje “ ”.
Generaliziramo li dobiveno pravilo na proizvoljnu linearnu funkciju, dobivamo sljedeći algoritam:
Kvadratna funkcija
Nadam se da se sjećate kako riješiti kvadratne nejednadžbe? Ako ne, pročitajte temu "Kvadratne nejednakosti." Da vas podsjetim na opći oblik kvadratne funkcije: .
Prisjetimo se sada koje predznake ima kvadratna funkcija. Njegov graf je parabola, a funkcija uzima znak " " za one u kojima je parabola iznad osi, i " " - ako je parabola ispod osi:
Ako funkcija ima nule (vrijednosti na kojima), parabola siječe os u dvije točke - korijene odgovarajuće kvadratne jednadžbe. Dakle, os je podijeljena u tri intervala, a predznaci funkcije se naizmjenično mijenjaju pri prolasku kroz svaki korijen.
Je li moguće nekako odrediti znakove bez crtanja parabole svaki put?
Podsjetimo se da se kvadratni trinom može faktorizirati:
Označimo korijene na osi:
Sjetimo se da se predznak funkcije može promijeniti samo kada prolazi kroz korijen. Iskoristimo ovu činjenicu: za svaki od tri intervala na koje je os podijeljena korijenima dovoljno je odrediti predznak funkcije samo u jednoj proizvoljno odabranoj točki: u ostalim točkama intervala predznak će biti isti .
U našem primjeru: na 3″> oba izraza u zagradama su pozitivna (zamjena, na primjer: 0″>). Stavili smo znak " " na os:
Pa, kada su (zamjena, na primjer) obje zagrade negativne, što znači da je umnožak pozitivan:
To je ono što je metoda intervala: znajući predznake faktora na svakom intervalu, određujemo predznak cijelog umnoška.
Razmotrimo i slučajeve kada funkcija nema nula ili ima samo jednu.
Ako njih nema, onda nema ni korijena. To znači da neće biti “prolaska kroz korijen”. To znači da funkcija uzima samo jedan predznak na cijelom brojevnom pravcu. Lako se može odrediti zamjenom u funkciju.
Ako postoji samo jedan korijen, parabola dodiruje os, pa se predznak funkcije ne mijenja pri prolasku kroz korijen. Koje pravilo možemo smisliti za takve situacije?
Ako faktorirate takvu funkciju, dobit ćete dva identična faktora:
A svaki izraz na kvadrat je nenegativan! Stoga se predznak funkcije ne mijenja. U takvim ćemo slučajevima korijen, pri prolasku kroz koji se znak ne mijenja, istaknuti tako da ga zaokružimo kvadratom:
Takav korijen nazvat ćemo višestruki.
Metoda intervala u nejednadžbama
Sada se svaka kvadratna nejednadžba može riješiti bez crtanja parabole. Dovoljno je samo postaviti predznake kvadratne funkcije na os i odabrati intervale ovisno o predznaku nejednadžbe. Na primjer:
Izmjerimo korijene na osi i postavimo znakove:
Trebamo dio osi sa znakom " "; budući da nejednakost nije stroga, sami korijeni također su uključeni u rješenje:
Sada razmotrite racionalnu nejednakost - nejednakost čije su obje strane racionalni izrazi (vidi “Racionalne jednadžbe”).
Primjer:
Svi faktori osim jednog su ovdje “linearni”, odnosno sadrže varijablu samo na prvu potenciju. Takvi linearni faktori su nam potrebni za primjenu intervalne metode - predznak se mijenja pri prolasku kroz njihove korijene. Ali množitelj uopće nema korijena. To znači da je uvijek pozitivna (uvjerite se sami), te stoga ne utječe na predznak cijele nejednadžbe. To znači da njime možemo podijeliti lijevu i desnu stranu nejednakosti i tako je se riješiti:
Sada je sve isto kao i s kvadratnim nejednadžbama: određujemo u kojim točkama svaki od faktora postaje nula, označavamo te točke na osi i raspoređujemo predznake. Želio bih vam skrenuti pozornost na vrlo važnu činjenicu:
U slučaju parnog broja činimo isto kao i prije: zaokružimo točku kvadratom i ne mijenjamo predznak pri prolasku kroz korijen. Ali u slučaju neparnog broja, ovo pravilo ne vrijedi: znak će se i dalje mijenjati kada prolazi kroz korijen. Stoga s takvim korijenom ne radimo ništa dodatno, kao da nije višestruki. Gornja pravila vrijede za sve parne i neparne potencije.
Što trebamo napisati u odgovoru?
Ako je izmjena znakova povrijeđena, morate biti vrlo oprezni, jer ako nejednakost nije stroga, odgovor bi trebao uključivati sve osjenčane točke. Ali neki od njih često stoje odvojeno, odnosno nisu uključeni u zasjenjeno područje. U ovom slučaju dodajemo ih odgovoru kao izolirane točke (u vitičastim zagradama):
Primjeri (odlučite sami):
odgovori:
- Ako je među faktorima jednostavan, to je korijen, jer se može prikazati kao.
.
Vrijednosti argumenata z na kojem f(z) ide na nulu tzv. nulta točka, tj. Ako f(a) = 0, tada a - nulta točka.
Def. Točka A nazvao nulti redn
, Ako
FKP se može prikazati u obliku f(z) = , gdje je 
analitičku funkciju i 
0.
U ovom slučaju, u proširenju funkcije (43) u Taylorov red, prvi n koeficijenti su nula
=
=
itd. Odredi red nule za 
i (1 –cos z) na z
=
0
=
=
nula 1. reda
1 – cos z
=
=
nula 2. reda
Def. Točka z
=
nazvao točka u beskonačnosti I nula funkcije f(z), Ako f(
) = 0. Takva se funkcija može proširiti u niz negativnih potencija z
: f(z)
=
. Ako
prvi n
koeficijenti jednaki nuli, tada dolazimo do nulti red n
u točki u beskonačnosti: f(z)
= z
-
n
.
Izolirane singularne točke dijele se na: a) uklonjive singularne točke; b) polovi redan; V) u biti singularne točke.
Točka A nazvao uklonjiva singularna točka funkcije f(z) ako na z 
a
lim f(z)
= sa - konačni broj .
Točka A nazvao stup redan
(n
1) funkcije f(z), ako je inverzna funkcija 
=
1/
f(z) ima nulti red n u točki A. Takva se funkcija uvijek može prikazati kao f(z)
=
, Gdje 
- analitička funkcija i 
.
Točka A nazvao u biti posebna točka funkcije f(z), ako na z 
a
lim f(z) ne postoji.
Laurentova serija
Razmotrimo slučaj regije konvergencije prstena r < | z 0 – a| < R centriran u točki A za funkciju f(z). Predstavimo dva nova kruga L 1 (r) I L 2 (R) u blizini granica prstena s točkom z 0 između njih. Izrežemo prsten, spojimo krugove duž rubova reza, prijeđemo na jednostavno spojeno područje i u
Cauchyjevom integralnom formulom (39) dobivamo dva integrala po varijabli z
f(z 0)
=
+
,
(42)
gdje integracija ide u suprotnim smjerovima.
Za integralni preko L 1 uvjet je ispunjen | z 0 – a | > | z – a |, i za integralni nad L 2 inverzni uvjet | z 0 – a | < | z – a |. Prema tome, faktor 1/( z – z 0) proširiti u niz (a) u integralu preko L 2 i u seriji (b) u integralnom nad L 1 . Kao rezultat toga, dobivamo ekspanziju f(z) u području prstena u Laurentova serija pozitivnim i negativnim potencijama ( z 0 – a)
f(z 0)
=
A n
(z 0 -a) n
(43)
Gdje A n
=
=
;A -n
=
Ekspanzija u pozitivnim moćima (z 0 - A) nazvao desni dio Laurentov red (Taylorov red), a proširenje u negativne potencije naziva se. glavni dio Laurentova serija.
Ako je unutar kruga L 1 nema singularnih točaka i funkcija je analitička, tada je u (44) prvi integral jednak nuli po Cauchyjevom teoremu i ostaje samo točan dio u proširenju funkcije. Negativne ovlasti u ekspanziji (45) pojavljuju se samo kada je analitičnost narušena unutar unutarnjeg kruga i služe za opisivanje funkcije u blizini izoliranih singularnih točaka.
Za konstruiranje Laurentovog niza (45) za f(z) možete izračunati koeficijente proširenja koristeći opću formulu ili koristiti proširenja elementarnih funkcija uključenih u f(z).
Broj termina ( n) glavnog dijela Laurentovog niza ovisi o vrsti singularne točke: uklonjiva singularna točka
(n
=
0)
; u biti singularna točka
(n 
);
poln- wow red(n
-
konačni broj).
i za f(z)
=
točka z
= 0 uklonjiva singularna točka, jer nema glavnog dijela. f(z)
=
(z
-
) = 1 -
b) Za f(z)
=
točka z
= 0 -
stup 1. reda
f(z)
=
(z
-
) =
-
c) Za f(z) = e 1 / z točka z = 0 - u biti singularna točka
f(z)
=
e 1 /
z =
Ako f(z) je analitička u domeni D uz iznimku m izolirane singularne točke 
i | z 1 |
< |z 2 |
< . . . < |z m| , zatim kod proširenja funkcije u ovlastima z cijela je ravnina podijeljena na m+ 1 prsten | z ja |
< | z
| < | z ja+ 1 | a serija Laurent ima drugačiji izgled za svaki prsten. Prilikom proširenja ovlasti ( z
–
z ja
) područje konvergencije Laurentovog niza je krug | z
–
z ja
| < r, Gdje r
– udaljenost do najbliže singularne točke.
itd. Proširimo funkciju f(z)
=
u seriji Laurent u moćima z i ( z
-
1).
Riješenje. Predstavimo funkciju u obliku f(z)
= - z 2
. Koristimo formulu za zbroj geometrijske progresije 
. U krugu |z|< 1 ряд сходится и f(z)
= - z 2
(1 + z
+ z 2
+ z 3
+ z 4
+ . . .) = - z 2
- z 3
- z 4 - . . . , tj. razgradnja sadrži samo ispraviti Dio. Prijeđimo na vanjsko područje kruga |z| > 1. Predstavimo funkciju u obliku 
, gdje je 1/| z|
< 1, и получим разложение f(z)
= z
=z
+ 1 +
Jer , proširenje funkcije u potencije ( z
-
1) izgleda f(z)
= (z
-
1) -1
+ 2 + (z
-
1) za sve 
1.
itd. Proširite funkciju u Laurentovu seriju f(z)
=
:
a) po stupnjevima z u krug | z|
< 1; b)
по степеням z
prsten 1<
|z|
< 3 ; c)
по степеням (z
–
2).Rješenje. Rastavimo funkciju na proste razlomke
=
=
+
=
.
Od uvjeta z
=1
A
= -1/2 , z
=3
B
= ½.
A) f(z)
=
½ [ 
]
= ½ [ 
-(1/3)
], s | z|<
1.
b) f(z)
= - ½ [ 
+
]
= -
(
), na 1< |z|
< 3.
S) f(z)
=
½ [ 
]= -
½
[ 
]
=
=
- ½
= -
, s |2 - z|
< 1
To je krug radijusa 1 sa središtem u z = 2 .
U nekim slučajevima, redovi potencija mogu se svesti na skup geometrijskih progresija, nakon čega je lako odrediti područje njihove konvergencije.
itd. Istražite konvergenciju niza
.
. . +
+
+
+
1
+ ()
+ ()
2
+ ()
3
+ . . .
Riješenje. Ovo je zbroj dviju geometrijskih progresija sa q 1
=
, q 2 = () . Iz uvjeta njihove konvergencije slijedi 
< 1 ,
< 1 или |z|
> 1 , |z|
< 2 , т.е. область сходимости ряда кольцо
1 < |z|
< 2 .
2. Nađimo nulte točke funkcije.
f(x) na x 
.
Odgovorite f(x) na x .
2) x 2 >-4x-5;
x 2 +4x +5>0;
Neka je f(x)=x 2 +4x +5 tada Nađimo takav x za koji je f(x)>0,
D=-4 Bez nula.
4. Sustavi nejednakosti. Nejednadžbe i sustavi nejednadžbi s dvije varijable
1) Skup rješenja sustava nejednadžbi je presjek skupova rješenja nejednadžbi koje su u njemu uključene.
2) Skup rješenja nejednadžbe f(x;y)>0 može se grafički prikazati na koordinatnoj ravnini. Tipično, pravac definiran jednadžbom f(x;y) = 0 dijeli ravninu na 2 dijela, od kojih je jedan rješenje nejednadžbe. Da biste odredili koji dio, potrebno je u nejednadžbu zamijeniti koordinate proizvoljne točke M(x0;y0) koja ne leži na pravcu f(x;y)=0. Ako je f(x0;y0) > 0, tada je rješenje nejednadžbe dio ravnine koji sadrži točku M0. ako je f(x0;y0)<0, то другая часть плоскости.
3) Skup rješenja sustava nejednadžbi je presjek skupova rješenja nejednadžbi koje su u njemu uključene. Neka nam je, na primjer, dan sustav nejednakosti:
.
Za prvu nejednadžbu skup rješenja je kružnica polumjera 2 sa središtem u ishodištu, a za drugu je to poluravnina koja se nalazi iznad pravca 2x+3y=0. Skup rješenja ovog sustava je presjek tih skupova, tj. polukrug.
4) Primjer. Riješite sustav nejednadžbi:
Rješenje 1. nejednadžbe je skup , 2. je skup (2;7) i treće je skup .
Sjecište tih skupova je interval (2;3], koji je skup rješenja sustava nejednadžbi.
5. Rješavanje racionalnih nejednadžbi metodom intervala
Metoda intervala temelji se na sljedećem svojstvu binoma (x-a): točka x = α dijeli brojevnu os na dva dijela - desno od točke α binom (x-α)>0, a na lijevo od točke α (x-α)<0.
Neka je potrebno riješiti nejednadžbu (x-α 1)(x-α 2)...(x-α n)>0, gdje su α 1, α 2 ...α n-1, α n fiksni brojevi među kojima nema jednakih i takvi da je α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 metodom intervala postupite na sljedeći način: brojevi α 1, α 2 ...α n-1, α n nanesu se na numeričku os; u intervalu desno od najvećeg od njih, tj. brojeva α n, stavite znak plus, u intervalu koji slijedi s desna na lijevo stavite znak minus, zatim znak plus, pa znak minus itd. Tada će skup svih rješenja nejednadžbe (x-α 1)(x‑α 2)...(x-α n)>0 biti unija svih intervala u kojima se nalazi znak plus, a skup rješenja nejednadžbe (x-α 1 )(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».
1) Rješavanje racionalnih nejednadžbi (tj. nejednakosti oblika 
P(x) Q(x) gdje su polinomi) temelji se na sljedećem svojstvu kontinuirane funkcije: ako kontinuirana funkcija nestaje u točkama x1 i x2 (x1; x2) i nema drugih korijena između tih točaka, tada u intervalima (x1; x2) funkcija zadržava predznak.
Stoga, da bismo pronašli intervale konstantnog predznaka funkcije y=f(x) na brojevnom pravcu, označimo sve točke u kojima funkcija f(x) nestaje ili trpi diskontinuitet. Te točke dijele brojevni pravac na nekoliko intervala, unutar kojih je funkcija f(x) neprekidna i ne nestaje, tj. sprema znak. Za određivanje ovog znaka dovoljno je pronaći znak funkcije u bilo kojoj točki razmatranog intervala brojevnog pravca.
2) Odrediti intervale konstantnog predznaka racionalne funkcije, tj. Da bismo riješili racionalnu nejednadžbu, na brojevnom pravcu označimo korijene brojnika i korijene nazivnika, koji su ujedno i korijeni i lomne točke racionalne funkcije.
Rješavanje nejednadžbi metodom intervala
3. 
< 20.
Riješenje. Raspon prihvatljivih vrijednosti određen je sustavom nejednakosti:
Za funkciju f(x) = – 20. Nađi f(x):
odakle je x = 29 i x = 13.
f(30) = – 20 = 0,3 > 0,
f(5) = – 1 – 20 = – 10< 0.
Odgovor: . Osnovne metode rješavanja racionalnih jednadžbi. 1) Najjednostavniji: rješava se uobičajenim pojednostavljenjima - svođenjem na zajednički nazivnik, svođenjem sličnih pojmova i tako dalje. Kvadratne jednadžbe ax2 + bx + c = 0 rješavaju se pomoću...
X se mijenja na intervalu (0,1], a smanjuje se na intervalu)