Funksioni zero. Zero e një funksioni Si të përcaktojmë zero të një funksioni
Funksioniështë një nga konceptet më të rëndësishme matematikore. Funksioni - varësia e ndryshueshme në nga ndryshorja x, nëse çdo vlerë X përputhet me një vlerë të vetme në. E ndryshueshme X quhet variabla ose argument i pavarur. E ndryshueshme në quhet ndryshorja e varur. Të gjitha vlerat e ndryshores së pavarur (ndryshore x) formojnë domenin e përkufizimit të funksionit. Të gjitha vlerat që merr ndryshorja e varur (ndryshore y), formojnë gamën e vlerave të funksionit.
Grafiku i funksionit thirrni grupin e të gjitha pikave të planit koordinativ, abshisat e të cilave janë të barabarta me vlerat e argumentit, dhe ordinatat janë të barabarta me vlerat përkatëse të funksionit, domethënë vlerat e variablat vizatohen përgjatë boshtit të abshisës x, dhe vlerat e ndryshores vizatohen përgjatë boshtit të ordinatave y. Për të grafikuar një funksion, duhet të dini vetitë e funksionit. Karakteristikat kryesore të funksionit do të diskutohen më poshtë!
Për të ndërtuar një grafik të një funksioni, ne rekomandojmë përdorimin e programit tonë - Funksionet grafikuese në internet. Nëse keni ndonjë pyetje gjatë studimit të materialit në këtë faqe, gjithmonë mund t'i bëni ato në forumin tonë. Gjithashtu në forum ata do t'ju ndihmojnë të zgjidhni problemet në matematikë, kimi, gjeometri, teori probabiliteti dhe shumë lëndë të tjera!
Vetitë themelore të funksioneve.
1) Domeni i funksionit dhe diapazoni i funksionit.
Domeni i një funksioni është grupi i të gjitha vlerave të vlefshme të argumentit x(ndryshueshme x), për të cilin funksioni y = f(x) të përcaktuara.
Gama e një funksioni është bashkësia e të gjitha vlerave reale y, të cilin funksioni e pranon.
Në matematikën elementare, funksionet studiohen vetëm në bashkësinë e numrave realë.
2) Funksioni zero.
Funksioni zero është vlera e argumentit në të cilin vlera e funksionit është e barabartë me zero.
3) Intervalet e shenjës konstante të një funksioni.
Intervalet e shenjës konstante të një funksioni janë grupe vlerash argumentesh mbi të cilat vlerat e funksionit janë vetëm pozitive ose vetëm negative.
4) Monotonia e funksionit.
Një funksion në rritje (në një interval të caktuar) është një funksion në të cilin një vlerë më e madhe e argumentit nga ky interval korrespondon me një vlerë më të madhe të funksionit.
Një funksion në rënie (në një interval të caktuar) është një funksion në të cilin një vlerë më e madhe e argumentit nga ky interval korrespondon me një vlerë më të vogël të funksionit.
5) Funksioni çift (tek)..
Një funksion çift është një funksion, domeni i përkufizimit të të cilit është simetrik në lidhje me origjinën dhe për cilindo X nga fusha e përkufizimit barazia f(-x) = f(x). Grafiku i një funksioni çift është simetrik ndaj ordinatës.
Një funksion tek është një funksion, domeni i përkufizimit të të cilit është simetrik në lidhje me origjinën dhe për cilindo X nga fusha e përkufizimit barazia është e vërtetë f(-x) = - f(x). Grafiku i një funksioni tek është simetrik në lidhje me origjinën.
6) Funksione të kufizuara dhe të pakufizuara.
Një funksion quhet i kufizuar nëse ka një numër pozitiv M të tillë që |f(x)| ≤ M për të gjitha vlerat e x. Nëse një numër i tillë nuk ekziston, atëherë funksioni është i pakufizuar.
7) Periodiciteti i funksionit.
Një funksion f(x) është periodik nëse ka një numër T jozero të tillë që për çdo x f(x+T) = f(x). Ky numër më i vogël quhet periudha e funksionit. Të gjitha funksionet trigonometrike janë periodike. (Formulat trigonometrike).
Pasi të keni studiuar këto veti të një funksioni, mund të eksploroni lehtësisht funksionin dhe, duke përdorur vetitë e funksionit, mund të ndërtoni një grafik të funksionit. Shikoni gjithashtu materialin për tabelën e së vërtetës, tabelën e shumëzimit, tabelën periodike, tabelën e derivateve dhe tabelën e integraleve.
Funksioni zero
Cilat janë zerat e funksionit? Si të përcaktohen zerot e një funksioni në mënyrë analitike dhe grafike?
Funksioni zero- këto janë vlerat e argumentit në të cilat funksioni është i barabartë me zero.
Për të gjetur zerot e funksionit të dhënë nga formula y=f(x), duhet të zgjidhni ekuacionin f(x)=0.
Nëse ekuacioni nuk ka rrënjë, funksioni nuk ka zero.
1) Gjeni zerot e funksionit linear y=3x+15.
Për të gjetur zerot e funksionit, zgjidhni ekuacionin 3x+15 =0.
Kështu, zeroja e funksionit është y=3x+15 - x= -5.
2) Gjeni zerot e funksionit kuadratik f(x)=x²-7x+12.
Për të gjetur zerot e funksionit, zgjidhni ekuacionin kuadratik
Rrënjët e tij x1=3 dhe x2=4 janë zero të këtij funksioni.
3) Gjeni zerot e funksionit
Një thyesë ka kuptim nëse emëruesi është jo zero. Prandaj, x²-1≠0, x² ≠ 1, x ≠±1. Kjo është, fusha e përkufizimit të një funksioni të caktuar (DO)
Nga rrënjët e ekuacionit x²+5x+4=0 x1=-1 x2=-4, vetëm x=-4 përfshihet në fushën e përkufizimit.
Për të gjetur zerot e një funksioni të dhënë grafikisht, duhet të gjeni pikat e prerjes së grafikut të funksionit me boshtin e abshisave.
Nëse grafiku nuk e pret boshtin Ox, funksioni nuk ka zero.
funksioni grafiku i të cilit është paraqitur në figurë ka katër zero -
Në algjebër, problemi i gjetjes së zerove të një funksioni shfaqet si si detyrë e pavarur ashtu edhe kur zgjidhen probleme të tjera, për shembull, kur studion një funksion, zgjidh pabarazitë, etj.
www.algebraclass.ru
Rregulli i funksionit zero
Konceptet themelore dhe vetitë e funksioneve
Rregulli (ligji i) korrespondencës. Funksioni monotonik .
Funksione të kufizuara dhe të pakufizuara. E vazhdueshme dhe
funksionet e ndërprera . Funksionet çift dhe tek.
Funksioni periodik. Periudha e funksionit.
Funksioni zero . Asimptotë .
Fusha e përkufizimit dhe diapazoni i vlerave të një funksioni. Në matematikën elementare, funksionet studiohen vetëm në bashkësinë e numrave realë R . Kjo do të thotë që argumenti i funksionit mund të marrë vetëm ato vlera reale për të cilat është përcaktuar funksioni, d.m.th. pranon edhe vetëm vlera reale. Një tufë me X të gjitha vlerat e vlefshme të argumentit x, për të cilin funksioni y = f (x) përcaktohet, quhet domeni i funksionit. Një tufë me Y të gjitha vlerat reale y, të cilin funksioni e pranon, quhet diapazoni i funksionit. Tani mund të japim një përkufizim më të saktë të funksionit: rregull (ligji) i korrespondencës ndërmjet grupeve X Dhe Y , sipas të cilit për çdo element nga bashkësia X ju mund të gjeni një dhe vetëm një element nga grupi Y, quhet funksion .
Nga ky përkufizim del se një funksion konsiderohet i përcaktuar nëse:
— specifikohet fusha e përcaktimit të funksionit X ;
— specifikohet diapazoni i funksionit Y ;
— rregulli (ligji) i korrespondencës është i njohur dhe i tillë që për secilin
vlera e argumentit, mund të gjendet vetëm një vlerë funksioni.
Kjo kërkesë e unike e funksionit është e detyrueshme.
Funksioni monotonik.
Nëse për çdo dy vlera të argumentit x 1 dhe x 2 të gjendjes x 2 > x 1 vijon f (x 2) > f (x 1), pastaj funksioni f (x) quhet në rritje; nëse për ndonjë x 1 dhe x 2 të gjendjes x 2 > x 1 vijon f (x 2)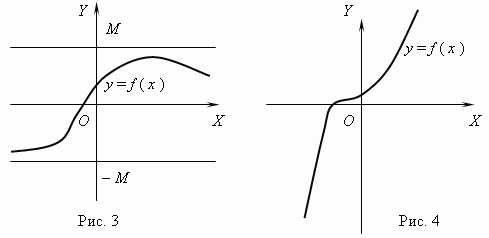 
Funksioni i paraqitur në Fig. 3 është i kufizuar, por jo monoton. Funksioni në figurën 4 është krejt i kundërt, monoton, por i pakufizuar. (Shpjegoni këtë ju lutem!).
Funksionet e vazhdueshme dhe jo të vazhdueshme. Funksioni y = f (x) quhet të vazhdueshme në pikën x = a, Nëse:
1) funksioni përcaktohet kur x = a, d.m.th. f (a) ekziston;
2) ekziston të fundme limit lim f (x) ;
Nëse të paktën një nga këto kushte nuk plotësohet, atëherë thirret funksioni eksplozive në pikën x = a .
Nëse funksioni është i vazhdueshëm gjatë të gjithë pikat e domenit të tij të përkufizimit, atëherë quhet funksion të vazhdueshëm.
Funksionet çift dhe tek. Nëse për ndonjë x nga fusha e përkufizimit të funksionit vlen sa vijon: f (— x) = f (x), atëherë thirret funksioni madje; nëse ndodh: f (— x) = — f (x), atëherë thirret funksioni i çuditshëm. Grafiku i një funksioni çift simetrike rreth boshtit Y(Fig. 5), një grafik i një funksioni tek Sim metrikë në lidhje me origjinën(Fig. 6).
Funksioni periodik. Funksioni f (x) — periodike, nëse një gjë e tillë ekziston jo zero numri T Per cfare ndonjë x nga fusha e përkufizimit të funksionit vlen sa vijon: f (x + T) = f (x). Kjo më së paku thirret numri periudha e funksionit. Të gjitha funksionet trigonometrike janë periodike.
Shembulli 1. Vërtetoni atë mëkat x ka një periudhë prej 2.
Zgjidhja: Ne e dimë se mëkati ( x+ 2 n) = mëkat x, Ku n= 0, ± 1, ± 2, …
Prandaj, shtesa 2 n jo për argumentin sinus
ndryshon vlerën e saj e. A ka ndonjë numër tjetër me këtë
Le të pretendojmë se P– një numër i tillë, d.m.th. barazi:
e vlefshme për çdo vlerë x. Por pastaj ka
vend dhe në x= / 2, d.m.th.
mëkat (/2 + P) = mëkat / 2 = 1.
Por sipas formulës së reduktimit sin (/ 2 + P) = cos P. Pastaj
nga dy barazitë e fundit rezulton se cos P= 1, por ne
ne e dimë se kjo është e vërtetë vetëm kur P = 2 n. Që nga më i vogli
numër jo zero nga 2 nështë 2, atëherë ky numër
dhe ka një mëkat të periudhës x. Mund të vërtetohet në mënyrë të ngjashme se 2
është gjithashtu një periudhë për cos x .
Vërtetoni se funksionet nxihen x dhe krevat fëmijësh x kanë periudhë .
Shembulli 2. Cili numër është periudha e funksionit sin 2 x ?
Zgjidhja: Merrni parasysh mëkatin 2 x= mëkat (2 x+ 2 n) = mëkat [ 2 ( x + n) ] .
Ne e shohim atë duke shtuar n ndaj argumentit x, nuk ndryshon
vlera e funksionit. Numri më i vogël jo zero
nga nështë , pra kjo është periudha mëkati 2 x .
Funksioni zero. Vlera e argumentit në të cilën funksioni është i barabartë me 0 thirret zero ( rrënja) funksion. Një funksion mund të ketë zero të shumta. Për shembull, funksioni y = x (x + 1) (x- 3) ka tre zero: x = 0, x = — 1, x= 3. Gjeometrikisht funksioni null – kjo është abshisa e pikës së prerjes së grafikut të funksionit me boshtin X .
Figura 7 tregon një grafik të një funksioni me zero: x = a , x = b Dhe x = c .
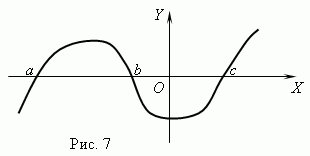
Asimptotë. Nëse grafiku i një funksioni i afrohet një vijë të caktuar për një kohë të pacaktuar ndërsa largohet nga origjina, atëherë kjo linjë quhet asimptotë.
Tema 6. “Metoda e intervalit”.
Nëse f (x) f (x 0) për x x 0, atëherë thirret funksioni f (x). e vazhdueshme në pikën x 0.
Nëse një funksion është i vazhdueshëm në çdo pikë të një intervali I, atëherë ai thirret e vazhdueshme në interval I (intervali I quhet intervali i vazhdimësisë së funksionit). Grafiku i një funksioni në këtë interval është një vijë e vazhdueshme, për të cilën ata thonë se mund të "vizatohet pa e hequr lapsin nga letra".
Vetia e funksioneve të vazhdueshme.
Nëse në intervalin (a ; b) funksioni f është i vazhdueshëm dhe nuk zhduket, atëherë ai ruan një shenjë konstante në këtë interval.
Një metodë për zgjidhjen e pabarazive me një ndryshore, metoda e intervalit, bazohet në këtë veti. Le të jetë funksioni f(x) i vazhdueshëm në intervalin I dhe të zhduket në një numër të kufizuar pikash në këtë interval. Nga vetia e funksioneve të vazhdueshme, këto pika e ndajnë I-në në intervale, në secilën prej të cilave funksioni i vazhdueshëm f(x) c mban një shenjë konstante. Për të përcaktuar këtë shenjë, mjafton të llogaritet vlera e funksionit f(x) në çdo pikë nga çdo interval i tillë. Bazuar në këtë, marrim algoritmin e mëposhtëm për zgjidhjen e pabarazive duke përdorur metodën e intervalit.
Metoda e intervalit për pabarazitë e formës
Metoda e intervalit. Niveli mesatar.
Dëshironi të provoni forcën tuaj dhe të zbuloni rezultatin se sa gati jeni për Provimin e Bashkuar të Shtetit ose Provimin e Unifikuar të Shtetit?
Funksioni linear
Një funksion i formës quhet linear. Le të marrim një funksion si shembull. Është pozitiv në 3″> dhe negativ në. Pika është zero e funksionit (). Le të tregojmë shenjat e këtij funksioni në boshtin e numrave:
Themi se "funksioni ndryshon shenjën kur kalon nëpër pikë".
Mund të shihet se shenjat e funksionit korrespondojnë me pozicionin e grafikut të funksionit: nëse grafiku është mbi boshtin, shenja është “ ”, nëse poshtë tij është “ ”.
Nëse e përgjithësojmë rregullin që rezulton në një funksion linear arbitrar, marrim algoritmin e mëposhtëm:
Funksioni kuadratik
Shpresoj të mbani mend se si të zgjidhni pabarazitë kuadratike? Nëse jo, lexoni temën "Pabarazitë kuadratike". Më lejoni t'ju kujtoj formën e përgjithshme të një funksioni kuadratik: .
Tani le të kujtojmë se cilat shenja merr funksioni kuadratik. Grafiku i tij është një parabolë, dhe funksioni merr shenjën " " për ato në të cilat parabola është mbi boshtin, dhe " " - nëse parabola është nën bosht:
Nëse një funksion ka zero (vlerat në të cilat), parabola kryqëzon boshtin në dy pika - rrënjët e ekuacionit kuadratik përkatës. Kështu, boshti ndahet në tre intervale, dhe shenjat e funksionit ndryshojnë në mënyrë alternative kur kalojnë nëpër secilën rrënjë.
A është e mundur të përcaktohen disi shenjat pa vizatuar një parabolë çdo herë?
Kujtojmë se një trinom katror mund të faktorizohet:
Le të shënojmë rrënjët në bosht:
Kujtojmë se shenja e një funksioni mund të ndryshojë vetëm kur kalon nëpër rrënjë. Le të përdorim këtë fakt: për secilin nga tre intervalet në të cilat boshti ndahet me rrënjë, mjafton të përcaktohet shenja e funksionit vetëm në një pikë të zgjedhur në mënyrë arbitrare: në pikat e mbetura të intervalit, shenja do të jetë e njëjtë. .
Në shembullin tonë: në 3″> të dyja shprehjet në kllapa janë pozitive (zëvendësojnë, për shembull: 0″>). Ne vendosim një shenjë " " në bosht:
Epo, kur (zëvendësoni, për shembull), të dy kllapat janë negative, që do të thotë se produkti është pozitiv:
Kjo është ajo që është metoda e intervalit: duke ditur shenjat e faktorëve në çdo interval, ne përcaktojmë shenjën e të gjithë produktit.
Le të shqyrtojmë edhe rastet kur funksioni nuk ka zero, ose vetëm një.
Nëse nuk janë aty, atëherë nuk ka rrënjë. Kjo do të thotë se nuk do të ketë "kalim nëpër rrënjë". Kjo do të thotë që funksioni merr vetëm një shenjë në të gjithë vijën numerike. Mund të përcaktohet lehtësisht duke e zëvendësuar atë në një funksion.
Nëse ka vetëm një rrënjë, parabola prek boshtin, kështu që shenja e funksionit nuk ndryshon kur kalon nëpër rrënjë. Çfarë rregulli mund të nxjerrim për situata të tilla?
Nëse faktorizoni një funksion të tillë, merrni dy faktorë identikë:
Dhe çdo shprehje në katror është jonegative! Prandaj, shenja e funksionit nuk ndryshon. Në raste të tilla do të theksojmë rrënjën, kur kalojmë nëpër të cilën shenja nuk ndryshon, duke e rrethuar me një katror:
Ne do ta quajmë një rrënjë të tillë shumëfisha.
Metoda e intervalit në pabarazitë
Tani çdo pabarazi kuadratike mund të zgjidhet pa vizatuar një parabolë. Mjafton vetëm vendosja e shenjave të funksionit kuadratik në bosht dhe përzgjedhja e intervaleve në varësi të shenjës së pabarazisë. Për shembull:
Le të matim rrënjët në bosht dhe të vendosim shenjat:
Na duhet pjesa e boshtit me shenjën " "; meqenëse pabarazia nuk është e rreptë, vetë rrënjët përfshihen gjithashtu në zgjidhje:
Tani merrni parasysh një pabarazi racionale - një pabarazi, të dyja anët e së cilës janë shprehje racionale (shih "Ekuacionet racionale").
Shembull:
Të gjithë faktorët përveç njërit janë "linearë" këtu, domethënë, ata përmbajnë një ndryshore vetëm në fuqinë e parë. Na duhen faktorë të tillë linearë për të aplikuar metodën e intervalit - shenja ndryshon kur kalon nëpër rrënjët e tyre. Por shumëzuesi nuk ka rrënjë fare. Kjo do të thotë se është gjithmonë pozitive (kontrollojeni vetë), dhe për këtë arsye nuk ndikon në shenjën e të gjithë pabarazisë. Kjo do të thotë që ne mund të ndajmë anën e majtë dhe të djathtë të pabarazisë me të, dhe kështu të shpëtojmë prej saj:
Tani gjithçka është njësoj siç ishte me pabarazitë kuadratike: ne përcaktojmë se në cilat pika secili prej faktorëve bëhet zero, shënojmë këto pika në bosht dhe rregullojmë shenjat. Dëshiroj të tërheq vëmendjen tuaj për një fakt shumë të rëndësishëm:
Në rastin e një numri çift veprojmë njësoj si më parë: rrethojmë pikën me katror dhe nuk e ndryshojmë shenjën kur kalojmë nga rrënjës. Por në rastin e një numri tek, ky rregull nuk zbatohet: shenja do të ndryshojë akoma kur kalon nëpër rrënjë. Prandaj, ne nuk bëjmë asgjë shtesë me një rrënjë të tillë, sikur të mos ishte shumëfish. Rregullat e mësipërme vlejnë për të gjitha fuqitë çift dhe tek.
Çfarë duhet të shkruajmë në përgjigje?
Nëse ndërrimi i shenjave është shkelur, duhet të jeni shumë të kujdesshëm, sepse nëse pabarazia nuk është e rreptë, përgjigja duhet të përfshijë të gjitha pikat me hije. Por disa prej tyre shpesh qëndrojnë të ndarë, domethënë nuk përfshihen në zonën e hijes. Në këtë rast, ne i shtojmë ato në përgjigje si pika të izoluara (në kllapa kaçurrelë):
Shembuj (vendosni vetë):
Përgjigjet:
- Nëse ndër faktorët është i thjeshtë, është rrënjë, sepse mund të paraqitet si.
.
Vlerat e argumentit z në të cilën f(z) shkon në zero të thirrur. pikë zero, d.m.th. Nëse f(a) = 0, atëherë a - pika zero.
Def. Pika A thirrur rendit zeron
, Nëse
FKP mund të përfaqësohet në formë f(z) = , ku 
funksioni analitik dhe 
0.
Në këtë rast, në serinë Taylor zgjerimi i funksionit (43), i pari n koeficientët janë zero
=
=
etj. Përcaktoni rendin e zeros për 
dhe (1 – koz z) në z
=
0
=
=
zero rendi i parë
1 – koz z
=
=
zero rendi i dytë
Def. Pika z
=
thirrur pikë në pafundësi Dhe zero funksione f(z), Nëse f(
) = 0. Një funksion i tillë mund të zgjerohet në një seri në fuqi negative z
: f(z)
=
. Nëse
së pari n
koeficientët janë të barabartë me zero, atëherë arrijmë në rendit zero n
në një pikë në pafundësi: f(z)
= z
-
n
.
Pikat e veçuara njëjëse ndahen në: a) pika singulare të lëvizshme; b) polet e renditn; V) pika në thelb njëjës.
Pika A thirrur pikë njëjës e lëvizshme funksione f(z) nëse në z 
a
lim f(z)
= Me - numri përfundimtar .
Pika A thirrur poli i renditn
(n
1) funksionet f(z), nëse funksioni i anasjelltë 
=
1/
f(z) ka rend zero n në pikën A. Një funksion i tillë gjithmonë mund të përfaqësohet si f(z)
=
, Ku 
- funksioni analitik dhe 
.
Pika A thirrur në thelb një pikë e veçantë funksione f(z), nëse në z 
a
lim f(z) nuk ekziston.
Seriali Laurent
Le të shqyrtojmë rastin e një rajoni të konvergjencës unazore r < | z 0 – a| < R të përqendruar në një pikë A për funksionin f(z). Le të prezantojmë dy qarqe të reja L 1 (r) Dhe L 2 (R) pranë kufijve të unazës me një pikë z 0 mes tyre. Le të bëjmë një prerje të unazës, të lidhim rrathët përgjatë skajeve të prerjes, të kalojmë në një rajon të lidhur thjesht dhe në
Formula integrale Cauchy (39) marrim dy integrale mbi ndryshoren z
f(z 0)
=
+
,
(42)
ku integrimi shkon në drejtime të kundërta.
Për mbi integrale L 1 kusht eshte plotesuar | z 0 – a | > | z – a |, dhe për mbi integrale L 2 gjendje e anasjelltë | z 0 – a | < | z – a |. Prandaj, faktori 1/( z – z 0) zgjerohet në seri (a) në mbi integrale L 2 dhe në serinë (b) në mbi integrale L 1 . Si rezultat, marrim zgjerimin f(z) në zonën e unazës në Seriali Laurent nga fuqitë pozitive dhe negative ( z 0 – a)
f(z 0)
=
A n
(z 0 -a) n
(43)
Ku A n
=
=
;A -n
=
Zgjerimi i fuqive pozitive (z 0 - A) thirri pjesa e duhur Seria Laurent (seri Taylor), dhe zgjerimi në fuqitë negative quhet. Pjesa kryesore Seriali Laurent.
Nëse brenda rrethit L 1 nuk ka pika singulare dhe funksioni është analitik, atëherë në (44) integrali i parë është i barabartë me zero nga teorema e Cauchy dhe vetëm pjesa e saktë mbetet në zgjerimin e funksionit. Fuqitë negative në zgjerim (45) shfaqen vetëm kur analiticiteti cenohet brenda rrethit të brendshëm dhe shërbejnë për të përshkruar funksionin pranë pikave të veçuara njëjës.
Për të ndërtuar serinë Laurent (45) për f(z) mund të llogaritni koeficientët e zgjerimit duke përdorur një formulë të përgjithshme ose të përdorni zgjerime të funksioneve elementare të përfshira në f(z).
Numri i termave ( n) e pjesës kryesore të serisë Laurent varet nga lloji i pikës njëjës: pikë njëjës e lëvizshme
(n
=
0)
; pikë në thelb njëjës
(n 
);
shtyllën- wow urdhër(n
-
numri përfundimtar).
dhe për f(z)
=
pika z
= 0 pikë njëjës e lëvizshme, sepse nuk ka asnjë pjesë kryesore. f(z)
=
(z
-
) = 1 -
b) Për f(z)
=
pika z
= 0 -
Shtylla e rendit të parë
f(z)
=
(z
-
) =
-
c) Për f(z) = e 1 / z pika z = 0 - pikë në thelb njëjës
f(z)
=
e 1 /
z =
Nëse f(z) është analitike në domen D me përjashtim të m pika të veçuara njëjës 
dhe | z 1 |
< |z 2 |
< . . . < |z m| , atëherë kur zgjerohet funksioni në fuqi z i gjithë avioni është i ndarë në m+ 1 unazë | z i |
< | z
| < | z i+ 1 | dhe seria Laurent ka një pamje të ndryshme për secilën unazë. Kur zgjerohet në pushtet ( z
–
z i
) rajoni i konvergjencës së serisë Laurent është rrethi | z
–
z i
| < r, Ku r
– distanca nga pika më e afërt njëjës.
etj. Le të zgjerojmë funksionin f(z)
=
në serinë Laurent në fuqi z Dhe ( z
-
1).
Zgjidhje. Le të paraqesim funksionin në formë f(z)
= - z 2
. Ne përdorim formulën për shumën e një progresion gjeometrik 
. Në rrethin |z|< 1 ряд сходится и f(z)
= - z 2
(1 + z
+ z 2
+ z 3
+ z 4
+ . . .) = - z 2
- z 3
- z 4 - . . . , d.m.th. zbërthimi përmban vetëm korrekte Pjesë. Le të kalojmë në rajonin e jashtëm të rrethit |z| > 1. Le të paraqesim funksionin në formë 
, ku 1/| z|
< 1, и получим разложение f(z)
= z
=z
+ 1 +
Sepse , zgjerimi i një funksioni në pushtet ( z
-
1) duket si f(z)
= (z
-
1) -1
+ 2 + (z
-
1) për të gjithë 
1.
etj. Zgjero funksionin në një seri Laurent f(z)
=
:
a) me shkallë z në një rreth | z|
< 1; b)
по степеням z
unaza 1<
|z|
< 3 ; c)
по степеням (z
–
2).Zgjidhje. Le ta zbërthejmë funksionin në thyesa të thjeshta
=
=
+
=
.
Nga kushtet z
=1
A
= -1/2 , z
=3
B
= ½.
A) f(z)
=
½ [ 
]
= ½ [ 
-(1/3)
], me | z|<
1.
b) f(z)
= - ½ [ 
+
]
= -
(
), në 1< |z|
< 3.
Me) f(z)
=
½ [ 
]= -
½
[ 
]
=
=
- ½
= -
, me |2 - z|
< 1
Është një rreth me rreze 1 me qendër në z = 2 .
Në disa raste, seritë e fuqisë mund të reduktohen në një grup progresionesh gjeometrike, dhe pas kësaj është e lehtë të përcaktohet rajoni i konvergjencës së tyre.
etj. Hulumtoni konvergjencën e serisë
.
. . +
+
+
+
1
+ ()
+ ()
2
+ ()
3
+ . . .
Zgjidhje. Kjo është shuma e dy progresioneve gjeometrike me q 1
=
, q 2 = () . Nga kushtet e konvergjencës së tyre rrjedh 
< 1 ,
< 1 или |z|
> 1 , |z|
< 2 , т.е. область сходимости ряда кольцо
1 < |z|
< 2 .
2. Le të gjejmë zerot e funksionit.
f(x) në x 
.
Përgjigjuni f(x) në x .
2) x 2 >-4x-5;
x 2 +4x +5>0;
Le të gjejmë f(x)=x 2 +4x +5, atëherë le të gjejmë x të tillë për të cilin f(x)>0,
D=-4 Nuk ka zero.
4. Sistemet e pabarazive. Pabarazitë dhe sistemet e inekuacioneve me dy ndryshore
1) Bashkësia e zgjidhjeve për një sistem pabarazish është kryqëzimi i grupeve të zgjidhjeve ndaj pabarazive të përfshira në të.
2) Bashkësia e zgjidhjeve të pabarazisë f(x;y)>0 mund të paraqitet grafikisht në planin koordinativ. Në mënyrë tipike, vija e përcaktuar nga ekuacioni f(x;y) = 0 e ndan rrafshin në 2 pjesë, njëra prej të cilave është zgjidhja e pabarazisë. Për të përcaktuar se cilën pjesë, duhet të zëvendësoni koordinatat e një pike arbitrare M(x0;y0) që nuk shtrihet në drejtëzën f(x;y)=0 në pabarazi. Nëse f(x0;y0) > 0, atëherë zgjidhja e pabarazisë është pjesa e rrafshit që përmban pikën M0. nëse f(x0;y0)<0, то другая часть плоскости.
3) Bashkësia e zgjidhjeve të një sistemi pabarazish është kryqëzimi i grupeve të zgjidhjeve ndaj pabarazive të përfshira në të. Le të jepet, për shembull, një sistem pabarazish:
.
Për pabarazinë e parë, bashkësia e zgjidhjeve është një rreth me rreze 2 dhe me qendër në origjinë, dhe për të dytën, është një gjysmërrafsh i vendosur mbi drejtëzën 2x+3y=0. Bashkësia e zgjidhjeve të këtij sistemi është kryqëzimi i këtyre bashkësive, d.m.th. gjysmërreth.
4) Shembull. Zgjidheni sistemin e pabarazive:
Zgjidhja e pabarazisë së parë është bashkësia , e dyta është bashkësia (2;7) dhe e treta është bashkësia .
Kryqëzimi i këtyre bashkësive është intervali (2;3], i cili është bashkësia e zgjidhjeve të sistemit të pabarazive.
5. Zgjidhja e inekuacioneve racionale duke përdorur metodën e intervalit
Metoda e intervaleve bazohet në vetinë e mëposhtme të binomit (x-a): pika x = α ndan boshtin numerik në dy pjesë - në të djathtë të pikës α binomi (x-α)>0, dhe në majtas nga pika α (x-α)<0.
Le të jetë e nevojshme të zgjidhet pabarazia (x-α 1)(x-α 2)...(x-α n)>0, ku α 1, α 2 ...α n-1, α n janë fikse numra, midis të cilëve nuk ka të barabartë, dhe të tillë që α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 duke përdorur metodën e intervalit veproni si më poshtë: numrat α 1, α 2 ...α n-1, α n vizatohen në boshtin numerik; në intervalin në të djathtë të më të madhit prej tyre, d.m.th. numrat α n, vendosni një shenjë plus, në intervalin pas tij nga e djathta në të majtë vendosni një shenjë minus, pastaj një shenjë plus, pastaj një shenjë minus, etj. Atëherë bashkësia e të gjitha zgjidhjeve të pabarazisë (x-α 1)(x‑α 2)...(x-α n)>0 do të jetë bashkimi i të gjitha intervaleve në të cilat vendoset shenja plus dhe bashkësia të zgjidhjeve të pabarazisë (x-α 1 )(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».
1) Zgjidhja e pabarazive racionale (d.m.th. pabarazitë e formës 
P(x) Q(x) ku janë polinomet) bazohet në vetinë e mëposhtme të një funksioni të vazhdueshëm: nëse një funksion i vazhdueshëm zhduket në pikat x1 dhe x2 (x1; x2) dhe nuk ka rrënjë të tjera midis këtyre pikave, atëherë në intervalet (x1; x2) funksioni ruan shenjën e tij.
Prandaj, për të gjetur intervalet e shenjës konstante të funksionit y=f(x) në vijën numerike, shënoni të gjitha pikat në të cilat funksioni f(x) zhduket ose pëson një ndërprerje. Këto pika e ndajnë vijën numerike në disa intervale, brenda secilit prej të cilave funksioni f(x) është i vazhdueshëm dhe nuk zhduket, d.m.th. kursen shenjën. Për të përcaktuar këtë shenjë, mjafton të gjesh shenjën e funksionit në çdo pikë të intervalit të konsideruar të vijës numerike.
2) Për të përcaktuar intervalet e shenjës konstante të një funksioni racional, d.m.th. Për të zgjidhur një pabarazi racionale, shënojmë në vijën numerike rrënjët e numëruesit dhe rrënjët e emëruesit, të cilat janë gjithashtu rrënjët dhe pikat e ndërprerjes së funksionit racional.
Zgjidhja e pabarazive duke përdorur metodën e intervalit
3. 
< 20.
Zgjidhje. Gama e vlerave të pranueshme përcaktohet nga sistemi i pabarazive:
Për funksionin f(x) = – 20. Gjeni f(x):
prej nga x = 29 dhe x = 13.
f(30) = – 20 = 0,3 > 0,
f(5) = – 1 – 20 = – 10< 0.
Përgjigje:. Metodat themelore për zgjidhjen e ekuacioneve racionale. 1) Më e thjeshta: zgjidhet me thjeshtësimet e zakonshme - reduktimi në një emërues të përbashkët, reduktimi i termave të ngjashëm, etj. Ekuacionet kuadratike ax2 + bx + c = 0 zgjidhen me...
X ndryshon në interval (0,1] dhe zvogëlohet në interval)