Funkcijske ničle. Ničla funkcije Kako določiti ničle funkcije
funkcija je eden najpomembnejših matematičnih konceptov. Funkcija - odvisnost spremenljivke pri iz spremenljivke x, če je vsaka vrednost X se ujema z eno samo vrednostjo pri. Spremenljivka X imenujemo neodvisna spremenljivka ali argument. Spremenljivka pri imenovana odvisna spremenljivka. Vse vrednosti neodvisne spremenljivke (spremenljivke x) tvorijo domeno definicije funkcije. Vse vrednosti, ki jih ima odvisna spremenljivka (spremenljivka l), tvorijo obseg vrednosti funkcije.
Funkcijski graf imenujemo množico vseh točk koordinatne ravnine, katerih abscise so enake vrednosti argumenta, ordinate pa enake ustreznim vrednostim funkcije, to je vrednostim spremenljivke so narisane vzdolž abscisne osi x, vrednosti spremenljivke pa so narisane vzdolž ordinatne osi l. Če želite prikazati graf funkcije, morate poznati lastnosti funkcije. Glavne lastnosti funkcije bomo obravnavali spodaj!
Za izgradnjo grafa funkcije priporočamo uporabo našega programa - Graf funkcij na spletu. Če imate med preučevanjem gradiva na tej strani kakršna koli vprašanja, jih lahko vedno postavite na našem forumu. Tudi na forumu vam bodo pomagali rešiti naloge iz matematike, kemije, geometrije, teorije verjetnosti in mnogih drugih predmetov!
Osnovne lastnosti funkcij.
1) Funkcijska domena in funkcijsko območje.
Domena funkcije je niz vseh veljavnih vrednosti argumentov x(spremenljivka x), za katero je funkcija y = f(x) odločen.
Območje funkcije je množica vseh realnih vrednosti l, ki jih funkcija sprejme.
V osnovni matematiki se funkcije preučujejo le na množici realnih števil.
2) Funkcijske ničle.
Funkcija nič je vrednost argumenta, pri kateri je vrednost funkcije enaka nič.
3) Intervali konstantnega predznaka funkcije.
Intervali konstantnega znaka funkcije so nizi vrednosti argumentov, na katerih so vrednosti funkcije samo pozitivne ali samo negativne.
4) Monotonost funkcije.
Naraščajoča funkcija (v določenem intervalu) je funkcija, pri kateri večja vrednost argumenta iz tega intervala ustreza večji vrednosti funkcije.
Padajoča funkcija (v določenem intervalu) je funkcija, pri kateri večji vrednosti argumenta iz tega intervala ustreza manjša vrednost funkcije.
5) Soda (liha) funkcija.
Soda funkcija je funkcija, katere domena definicije je simetrična glede na izvor in za poljubno X s področja definicije enakost f(-x) = f(x). Graf sode funkcije je simetričen glede na ordinato.
Liha funkcija je funkcija, katere domena definicije je simetrična glede na izvor in za poljubno X s področja definicije velja enakost f(-x) = - f(x). Graf lihe funkcije je simetričen glede na izvor.
6) Omejene in neomejene funkcije.
Funkcija se imenuje omejena, če obstaja pozitivno število M tako, da |f(x)| ≤ M za vse vrednosti x. Če takšno število ne obstaja, je funkcija neomejena.
7) Periodičnost funkcije.
Funkcija f(x) je periodična, če obstaja neničelno število T tako, da je za vsak x f(x+T) = f(x). To najmanjše število imenujemo perioda funkcije. Vse trigonometrične funkcije so periodične. (Trigonometrične formule).
Ko preučite te lastnosti funkcije, lahko preprosto raziščete funkcijo in z uporabo lastnosti funkcije sestavite graf funkcije. Oglejte si tudi gradivo o resnicni tabeli, množilni tabeli, periodnem sistemu, tabeli odvodov in tabeli integralov.
Funkcijske ničle
Kaj so funkcijske ničle? Kako analitično in grafično določiti ničle funkcije?
Funkcijske ničle- to so vrednosti argumentov, pri katerih je funkcija enaka nič.
Če želite najti ničle funkcije, podane s formulo y=f(x), morate rešiti enačbo f(x)=0.
Če enačba nima korenin, funkcija nima ničel.
1) Poiščite ničle linearne funkcije y=3x+15.
Če želite najti ničle funkcije, rešite enačbo 3x+15 =0.
Tako je ničla funkcije y=3x+15 - x= -5.
2) Poiščite ničle kvadratne funkcije f(x)=x²-7x+12.
Če želite najti ničle funkcije, rešite kvadratno enačbo
Njeni korenini x1=3 in x2=4 sta ničli te funkcije.
3) Poiščite ničle funkcije
Ulomek je smiseln, če je imenovalec različen od nič. Zato je x²-1≠0, x² ≠ 1, x ≠±1. To je domena definicije dane funkcije (DO)
Od korenov enačbe x²+5x+4=0 x1=-1 x2=-4 je samo x=-4 vključeno v domeno definicije.
Če želite najti ničle funkcije, podane grafično, morate najti točke presečišča grafa funkcije z osjo abscise.
Če graf ne seka osi Ox, funkcija nima ničel.
funkcija, katere graf je prikazan na sliki, ima štiri ničle -
V algebri se problem iskanja ničel funkcije pojavlja tako kot samostojna naloga kot pri reševanju drugih problemov, na primer pri preučevanju funkcije, reševanju neenakosti itd.
www.algebraclass.ru
Pravilo funkcijskih ničel
Osnovni pojmi in lastnosti funkcij
Pravilo (pravo o) dopisovanju. Monotona funkcija .
Omejene in neomejene funkcije. Neprekinjeno in
diskontinuirana funkcija . Sode in lihe funkcije.
Periodična funkcija. Obdobje funkcije.
Funkcijske ničle . Asimptota .
Domena definicije in območje vrednosti funkcije. V osnovni matematiki se funkcije preučujejo le na množici realnih števil R . To pomeni, da lahko argument funkcije sprejme samo tiste realne vrednosti, za katere je funkcija definirana, tj. sprejema tudi samo prave vrednote. Kup X vse veljavne veljavne vrednosti argumentov x, za katerega funkcija l = f (x) je definiran, imenovan domena funkcije. Kup Y vse prave vrednosti l, ki ga funkcija sprejme, se imenuje obseg delovanja. Zdaj lahko podamo natančnejšo definicijo funkcije: pravilo (zakon) korespondence med množicami X in Y , po kateri za vsak element iz množice X lahko najdete en in samo en element iz nabora Y, se imenuje funkcija .
Iz te definicije sledi, da je funkcija definirana, če:
— določena je domena definicije funkcije X ;
— določeno je območje delovanja Y ;
— znano je pravilo (zakon) dopisovanja in tako, da za vsak
vrednost argumenta, je mogoče najti samo eno vrednost funkcije.
Ta zahteva po nedvoumnosti funkcije je obvezna.
Monotona funkcija.
Če za kateri koli dve vrednosti argumenta x 1 in x 2 pogoja x 2 > x 1 sledi f (x 2) > f (x 1), nato funkcijo f (x) je poklican povečevanje; če za kakšno x 1 in x 2 pogoja x 2 > x 1 sledi f (x 2)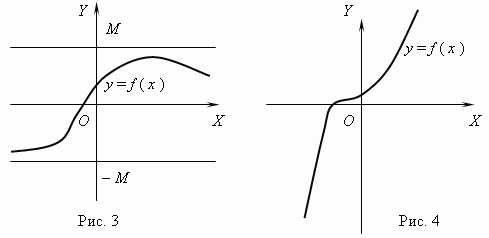 
Funkcija, prikazana na sliki 3, je omejena, vendar ni monotona. Funkcija na sliki 4 je ravno nasprotna, monotona, a neomejena. (Prosim, razložite to!).
Kontinuirane in diskontinuirane funkcije. funkcija l = f (x) je poklican neprekinjeno na točki x = a, Če:
1) funkcija je definirana, ko x = a, tj. f (a) obstaja;
2) obstaja končno limit lim f (x) ;
Če vsaj eden od teh pogojev ni izpolnjen, se funkcija pokliče eksplozivno na točki x = a .
Če je funkcija med vsi točke njene definicijske domene, potem se imenuje neprekinjena funkcija.
Sode in lihe funkcije. Če za kaj x iz domene definicije funkcije velja: f (— x) = f (x), nato se funkcija pokliče celo; če se zgodi: f (— x) = — f (x), nato se funkcija pokliče Čuden. Graf sode funkcije simetrično glede na os Y(slika 5), graf lihe funkcije Sim metrika glede na izvor(slika 6).
Periodična funkcija. funkcija f (x) — periodično, če kaj takega obstaja različen od ničštevilo T kaj za kaj x iz domene definicije funkcije velja: f (x + T) = f (x). to vsajštevilka je poklicana obdobje funkcije. Vse trigonometrične funkcije so periodične.
Primer 1. Dokaži ta greh x ima obdobje 2.
Rešitev: Vemo, da greh ( x+ 2 n) = greh x, Kje n= 0, ± 1, ± 2, …
Torej dodatek 2 n na sinusni argument
spremeni svojo vrednost e. Ali obstaja še ena številka s tem
Pretvarjajmo se, da p– takšno število, tj. enakost:
velja za katero koli vrednost x. Ampak potem je
mesto in pri x= / 2, tj.
greh (/2 + p) = greh / 2 = 1.
Toda po redukcijski formuli sin (/ 2 + p) = cos p. Potem
iz zadnjih dveh enakosti sledi, da je cos p= 1, ampak mi
vemo, da je to res šele, ko p = 2 n. Od najmanjšega
neničelno število od 2 n je 2, potem je to število
in obstaja mesečni greh x. Na podoben način je mogoče dokazati, da 2
je tudi obdobje za cos x .
Dokaži, da so funkcije tan x in posteljica x imeti menstruacijo.
Primer 2. Katero število je perioda funkcije sin 2 x ?
Rešitev: Razmislite o grehu 2 x= greh(2 x+ 2 n) = sin [ 2 ( x + n) ] .
Vidimo, da se dodaja n na argument x, se ne spremeni
vrednost funkcije. Najmanjše število, ki ni nič
od n je , torej je to obdobje sin 2 x .
Funkcijske ničle. Pokliče se vrednost argumenta, pri kateri je funkcija enaka 0 nič ( root) funkcijo. Funkcija ima lahko več ničel. Na primer funkcija l = x (x + 1) (x- 3) ima tri ničle: x = 0, x = — 1, x= 3. Geometrijsko ničelna funkcija – to je abscisa točke presečišča grafa funkcije z osjo X .
Slika 7 prikazuje graf funkcije z ničlami: x = a , x = b in x = c .
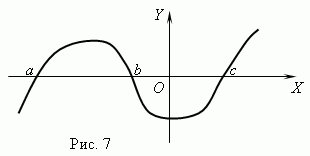
Asimptota. Če se graf funkcije neomejeno približuje določeni premici, ko se odmika od izhodišča, se ta premica imenuje asimptota.
Tema 6. “Intervalna metoda.”
Če je f (x) f (x 0) za x x 0, se pokliče funkcija f (x). zvezna v točki x 0.
Če je funkcija zvezna v vsaki točki nekega intervala I, se imenuje neprekinjeno na intervalu I (interval I se imenuje interval zveznosti funkcije). Graf funkcije na tem intervalu je neprekinjena črta, za katero pravijo, da jo je mogoče "narisati, ne da bi dvignili svinčnik s papirja."
Lastnost zveznih funkcij.
Če je na intervalu (a ; b) funkcija f zvezna in ne izniči, potem ohrani na tem intervalu konstanten predznak.
Na tej lastnosti temelji metoda za reševanje neenačb z eno spremenljivko, intervalna metoda. Naj bo funkcija f(x) zvezna na intervalu I in izniči na končnem številu točk v tem intervalu. Zaradi lastnosti zveznih funkcij te točke razdelijo I na intervale, v vsakem od katerih zvezna funkcija f(x) c ohranja konstanten predznak. Za določitev tega znaka je dovolj, da izračunamo vrednost funkcije f(x) v kateri koli točki iz vsakega takega intervala. Na podlagi tega dobimo naslednji algoritem za reševanje neenačb z intervalno metodo.
Intervalna metoda za neenakosti oblike
Intervalna metoda. Povprečna raven.
Ali želite preizkusiti svojo moč in ugotoviti, kako pripravljeni ste na enotni državni izpit ali enotni državni izpit?
Linearna funkcija
Funkcija oblike se imenuje linearna. Vzemimo za primer funkcijo. Pozitiven je pri 3″> in negativen pri. Pika je ničla funkcije (). Pokažimo znake te funkcije na številski osi:
Pravimo, da "funkcija pri prehodu skozi točko spremeni predznak".
Vidimo, da predznaki funkcije ustrezajo položaju grafa funkcije: če je graf nad osjo, je predznak “ ”, če je pod njo pa “ ”.
Če dobljeno pravilo posplošimo na poljubno linearno funkcijo, dobimo naslednji algoritem:
Kvadratna funkcija
Upam, da se spomnite, kako rešiti kvadratne neenačbe? Če ne, preberite temo "Kvadratne neenakosti." Naj vas spomnim na splošno obliko kvadratne funkcije: .
Zdaj pa se spomnimo, katere predznake ima kvadratna funkcija. Njen graf je parabola, funkcija pa ima znak " " za tiste, pri katerih je parabola nad osjo, in " " - če je parabola pod osjo:
Če ima funkcija ničle (vrednosti, pri katerih), parabola seka os v dveh točkah - koreninah ustrezne kvadratne enačbe. Tako je os razdeljena na tri intervale, pri prehodu skozi vsak koren pa se znaki funkcije izmenično spreminjajo.
Ali je mogoče nekako določiti znake, ne da bi vsakič narisali parabolo?
Spomnimo se, da je kvadratni trinom mogoče faktorizirati:
Označimo korenine na osi:
Spomnimo se, da se predznak funkcije lahko spremeni le pri prehodu skozi koren. Uporabimo to dejstvo: za vsakega od treh intervalov, na katere je os razdeljena s koreninami, je dovolj, da določimo predznak funkcije samo v eni poljubno izbrani točki: v preostalih točkah intervala bo predznak enak .
V našem primeru: pri 3″> sta oba izraza v oklepaju pozitivna (nadomestite, na primer: 0″>). Na os postavimo znak " ":
No, ko sta (na primer nadomestek) oba oklepaja negativna, kar pomeni, da je produkt pozitiven:
Tako je intervalna metoda: ob poznavanju predznakov faktorjev na vsakem intervalu določimo predznak celotnega produkta.
Upoštevajmo tudi primere, ko funkcija nima ničel ali ima samo eno.
Če jih ni, potem ni korenin. To pomeni, da ne bo "prehajanja skozi koren". To pomeni, da ima funkcija samo en predznak na celotni številski premici. Lahko ga enostavno določimo tako, da ga nadomestimo s funkcijo.
Če je koren samo en, se parabola dotika osi, zato se predznak funkcije pri prehodu skozi koren ne spremeni. Kakšno pravilo si lahko izmislimo za takšne situacije?
Če faktorizirate takšno funkcijo, dobite dva enaka faktorja:
In vsak izraz na kvadrat je nenegativen! Zato se predznak funkcije ne spremeni. V takih primerih bomo koren, pri prehodu skozi katerega se znak ne spremeni, poudarili tako, da ga obkrožimo s kvadratom:
Takšen koren bomo imenovali večkratniki.
Intervalna metoda v neenačbah
Vsako kvadratno neenakost je mogoče rešiti brez risanja parabole. Dovolj je, da na osi postavite znake kvadratne funkcije in izberete intervale glede na znak neenakosti. Na primer:
Izmerimo korenine na osi in postavimo znake:
Potrebujemo del osi z znakom " "; ker neenakost ni stroga, so v rešitev vključene tudi same korenine:
Zdaj razmislite o racionalni neenakosti - neenakosti, katere obe strani sta racionalna izraza (glejte "Racionalne enačbe").
primer:
Vsi faktorji razen enega so tukaj "linearni", to pomeni, da vsebujejo spremenljivko samo na prvo potenco. Takšne linearne faktorje potrebujemo za uporabo intervalne metode - predznak se spremeni pri prehodu skozi njihove korenine. Toda množitelj sploh nima korenin. To pomeni, da je vedno pozitivna (to preverite sami) in torej ne vpliva na predznak celotne neenakosti. To pomeni, da lahko z njim delimo levo in desno stran neenakosti in se je tako znebimo:
Zdaj je vse tako kot pri kvadratnih neenakostih: določimo, v katerih točkah vsak faktor postane nič, te točke označimo na osi in razporedimo predznake. Rad bi vas opozoril na zelo pomembno dejstvo:
Pri sodem številu naredimo enako kot prej: okoli točke narišemo kvadrat in pri prehodu skozi koren ne spremenimo predznaka. Toda v primeru lihe številke to pravilo ne velja: znak se bo še vedno spremenil, ko gre skozi koren. Zato s takim korenom ne naredimo nič dodatnega, kot da ne bi bil večkratnik. Zgornja pravila veljajo za vse sode in lihe potence.
Kaj naj zapišemo v odgovor?
Če je menjava znakov kršena, morate biti zelo previdni, kajti če neenakost ni stroga, mora odgovor vključevati vse zasenčene točke. Toda nekateri od njih pogosto stojijo ločeno, to pomeni, da niso vključeni v osenčeno območje. V tem primeru jih odgovoru dodamo kot izolirane točke (v zavitih oklepajih):
Primeri (odločite se sami):
odgovori:
- Če je med dejavniki preprost, je koren, ker ga lahko predstavimo kot.
.
Vrednosti argumentov z pri katerem f(z) gre na nič klicano. ničelna točka, tj. če f(a) = 0, torej a - ničelna točka.
Def. Pika A klical ničelni redn
, Če
FKP je mogoče predstaviti v obliki f(z) = , kjer 
analitično funkcijo in 
0.
V tem primeru je v Taylorjevem nizu razširitev funkcije (43) prva n koeficienti so nič
=
=
itd. Določite vrstni red nič za 
in (1 –cos z) pri z
=
0
=
=
nič 1. reda
1 – cos z
=
=
nič 2. reda
Def. Pika z
=
klical točka v neskončnost in nič funkcije f(z), če f(
) = 0. Takšno funkcijo lahko razširimo v niz v negativnih potencah z
: f(z)
=
. če
prvi n
koeficienti enaki nič, potem pridemo do ničelni red n
v točki v neskončnosti: f(z)
= z
-
n
.
Izolirane singularne točke delimo na: a) odstranljive singularne točke; b) poli redan; V) v bistvu singularne točke.
Pika A klical odstranljiva singularna točka funkcije f(z) če pri z 
a
lim f(z)
= z - končna številka .
Pika A klical pol redan
(n
1) funkcije f(z), če je inverzna funkcija 
=
1/
f(z) ima ničelni vrstni red n na točki A. Takšno funkcijo lahko vedno predstavimo kot f(z)
=
, Kje 
- analitična funkcija in 
.
Pika A klical v bistvu posebna točka funkcije f(z), če pri z 
a
lim f(z) ne obstaja.
Serija Laurent
Oglejmo si primer konvergenčnega območja obroča r < | z 0 – a| < R s središčem v točki A za funkcijo f(z). Predstavimo dva nova kroga L 1 (r) In L 2 (R) blizu meja obroča s točko z 0 med njimi. Izrežemo prstan, povežemo kroge ob robovih reza, preidemo na preprosto povezano območje in v
Cauchyjeva integralska formula (39) dobimo dva integrala po spremenljivki z
f(z 0)
=
+
,
(42)
kjer gre integracija v nasprotni smeri.
Za integral čez L 1 pogoj je izpolnjen | z 0 – a | > | z – a |, in za integral nad L 2 inverzni pogoj | z 0 – a | < | z – a |. Zato je faktor 1/( z – z 0) razširi v vrsto (a) v integralu čez L 2 in v seriji (b) v integralu nad L 1. Kot rezultat dobimo razširitev f(z) v območju obroča v Serija Laurent s pozitivnimi in negativnimi močmi ( z 0 – a)
f(z 0)
=
A n
(z 0 -a) n
(43)
Kje A n
=
=
;A -n
=
Razširitev pozitivnih moči (z 0 - A) klical desni del Laurentova vrsta (Taylorjeva vrsta) in raztezanje v negativnih potencah se imenuje. glavni del Serija Laurent.
Če je znotraj kroga L 1 ni singularnih točk in je funkcija analitična, potem je v (44) prvi integral po Cauchyjevem izreku enak nič in v razširitvi funkcije ostane samo pravilni del. Negativne moči v ekspanziji (45) se pojavijo le, ko je porušena analitičnost znotraj notranjega kroga in služijo za opis funkcije v bližini izoliranih singularnih točk.
Za konstruiranje Laurentove serije (45) za f(z) koeficiente razširitve lahko izračunate s splošno formulo ali uporabite razširitve elementarnih funkcij, vključenih v f(z).
Število terminov ( n) glavnega dela Laurentove vrste je odvisno od vrste singularne točke: odstranljiva singularna točka
(n
=
0)
; v bistvu singularna točka
(n 
);
palican- vau naročilo(n
-
končna številka).
in za f(z)
=
pika z
= 0 odstranljiva singularna točka, Ker ni glavnega dela. f(z)
=
(z
-
) = 1 -
b) Za f(z)
=
pika z
= 0 -
drog 1. reda
f(z)
=
(z
-
) =
-
c) Za f(z) = e 1 / z pika z = 0 - v bistvu singularna točka
f(z)
=
e 1 /
z =
če f(z) je analitičen v domeni D z izjemo m izolirane singularne točke 
in | z 1 |
< |z 2 |
< . . . < |z m| , potem pa ob razširitvi funkcije v pooblastilih z celotno letalo je razdeljeno na m+ 1 prstan | z jaz |
< | z
| < | z jaz+ 1 | in serija Laurent ima drugačen videz za vsak prstan. Pri širitvi pooblastil ( z
–
z jaz
) območje konvergence Laurentove vrste je krog | z
–
z jaz
| < r, Kje r
– razdalja do najbližje singularne točke.
itd. Razširimo funkcijo f(z)
=
v seriji Laurent v moči z In ( z
-
1).
rešitev. Predstavimo funkcijo v obliki f(z)
= - z 2
. Uporabimo formulo za vsoto geometrijske progresije 
. V krogu |z|< 1 ряд сходится и f(z)
= - z 2
(1 + z
+ z 2
+ z 3
+ z 4
+ . . .) = - z 2
- z 3
- z 4 - . . . , tj. razpad vsebuje samo pravilno del Premaknimo se na zunanje območje kroga |z| > 1. Predstavimo funkcijo v obliki 
, kjer je 1/| z|
< 1, и получим разложение f(z)
= z
=z
+ 1 +
Ker , razširitev funkcije v potencah ( z
-
1) izgleda f(z)
= (z
-
1) -1
+ 2 + (z
-
1) za vse 
1.
itd. Razširite funkcijo v niz Laurent f(z)
=
:
a) po stopinjah z v krogu | z|
< 1; b)
по степеням z
prstan 1<
|z|
< 3 ; c)
по степеням (z
–
2).Rešitev. Razčlenimo funkcijo na preproste ulomke
=
=
+
=
.
Od pogojev z
=1
A
= -1/2 , z
=3
B
= ½.
A) f(z)
=
½ [ 
]
= ½ [ 
-(1/3)
], z | z|<
1.
b) f(z)
= - ½ [ 
+
]
= -
(
), ob 1< |z|
< 3.
z) f(z)
=
½ [ 
]= -
½
[ 
]
=
=
- ½
= -
, z |2 - z|
< 1
To je krog s polmerom 1 s središčem z = 2 .
V nekaterih primerih je močenjsko vrsto mogoče zmanjšati na niz geometrijskih progresij, po tem pa je enostavno določiti območje njihove konvergence.
itd. Raziščite konvergenco vrste
.
. . +
+
+
+
1
+ ()
+ ()
2
+ ()
3
+ . . .
rešitev. To je vsota dveh geometrijskih progresij z q 1
=
, q 2 = () . Iz pogojev njihove konvergence sledi 
< 1 ,
< 1 или |z|
> 1 , |z|
< 2 , т.е. область сходимости ряда кольцо
1 < |z|
< 2 .
2. Poiščimo ničle funkcije.
f(x) pri x 
.
Odgovori f(x) pri x .
2) x 2 >-4x-5;
x 2 +4x +5>0;
Naj bo f(x)=x 2 +4x +5, potem najdemo tak x, za katerega je f(x)>0,
D=-4 Brez ničel.
4. Sistemi neenačb. Neenačbe in sistemi neenačb z dvema spremenljivkama
1) Množica rešitev sistema neenačb je presečišče množic rešitev neenačb, ki so vanj vključene.
2) Množico rešitev neenačbe f(x;y)>0 lahko grafično prikažemo na koordinatni ravnini. Običajno premica, definirana z enačbo f(x;y) = 0, deli ravnino na 2 dela, od katerih je eden rešitev neenačbe. Da bi ugotovili kateri del, morate v neenačbo nadomestiti koordinate poljubne točke M(x0;y0), ki ne leži na premici f(x;y)=0. Če je f(x0;y0) > 0, potem je rešitev neenačbe del ravnine, ki vsebuje točko M0. če f(x0;y0)<0, то другая часть плоскости.
3) Množica rešitev sistema neenačb je presečišče množic rešitev neenačb, ki so vanj vključene. Naj nam bo na primer dan sistem neenakosti:
.
Za prvo neenačbo je množica rešitev krog s polmerom 2 in s središčem v izhodišču, za drugo pa je polravnina, ki se nahaja nad premico 2x+3y=0. Množica rešitev tega sistema je presečišče teh množic, tj. polkrog.
4) Primer. Rešite sistem neenačb:
Rešitev 1. neenačbe je množica , 2. je množica (2;7) in tretja je množica .
Presek teh množic je interval (2;3], ki je množica rešitev sistema neenačb.
5. Reševanje racionalnih neenačb z intervalno metodo
Metoda intervalov temelji na naslednji lastnosti binoma (x-a): točka x = α deli številsko os na dva dela - desno od točke α je binom (x-α)>0, na levo od točke α (x-α)<0.
Naj bo treba rešiti neenačbo (x-α 1)(x-α 2)...(x-α n)>0, kjer so α 1, α 2 ...α n-1, α n fiksni števila, med katerimi ni enakih in taka, da je α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 z uporabo intervalne metode nadaljujte na naslednji način: števila α 1, α 2 ...α n-1, α n so narisana na numerični osi; v intervalu desno od največjega med njimi, tj. števila α n, postavite znak plus, v intervalu, ki mu sledi od desne proti levi, postavite znak minus, nato znak plus, nato znak minus itd. Potem bo množica vseh rešitev neenačbe (x-α 1)(x‑α 2)...(x-α n)>0 unija vseh intervalov, v katerih je znak plus, in množica rešitev neenačbe (x-α 1 )(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».
1) Reševanje racionalnih neenačb (tj. neenakosti oblike 
P(x) Q(x) kjer so polinomi) temelji na naslednji lastnosti zvezne funkcije: če zvezna funkcija izgine v točkah x1 in x2 (x1; x2) in med tema točkama nima drugih korenin, potem v intervalih (x1; x2) funkcija ohrani predznak.
Če želite torej na številski premici najti intervale konstantnega predznaka funkcije y=f(x), označite vse točke, v katerih funkcija f(x) izgine ali ima diskontinuiteto. Te točke delijo številsko premico na več intervalov, znotraj katerih je funkcija f(x) zvezna in ne izniči, tj. shrani znak. Za določitev tega znaka je dovolj, da poiščemo znak funkcije na kateri koli točki obravnavanega intervala številske črte.
2) Določiti intervale konstantnega predznaka racionalne funkcije, tj. Za rešitev racionalne neenačbe označimo na številski premici korenine števca in korenine imenovalca, ki so hkrati korenine in prelomne točke racionalne funkcije.
Reševanje neenačb z intervalno metodo
3. 
< 20.
rešitev. Razpon sprejemljivih vrednosti je določen s sistemom neenakosti:
Za funkcijo f(x) = – 20. Poišči f(x):
od koder je x = 29 in x = 13.
f(30) = – 20 = 0,3 > 0,
f(5) = – 1 – 20 = – 10< 0.
Odgovor: . Osnovne metode reševanja racionalnih enačb. 1) Najenostavnejši: rešuje se z običajnimi poenostavitvami - redukcija na skupni imenovalec, redukcija podobnih členov itd. Kvadratne enačbe ax2 + bx + c = 0 rešimo z...
X se spreminja na intervalu (0,1] in se na intervalu zmanjšuje)