ფუნქცია ნულები. ფუნქციის ნული როგორ განვსაზღვროთ ფუნქციის ნულები

ფუნქციაარის ერთ-ერთი ყველაზე მნიშვნელოვანი მათემატიკური ცნება. ფუნქცია - ცვლადი დამოკიდებულება ზეცვლადიდან x, თუ თითოეული მნიშვნელობა Xშეესაბამება ერთ მნიშვნელობას ზე. ცვლადი Xდამოუკიდებელი ცვლადი ან არგუმენტი ეწოდება. ცვლადი ზედამოკიდებულ ცვლადს უწოდებენ. დამოუკიდებელი ცვლადის ყველა მნიშვნელობა (ცვლადი x) ფუნქციის განსაზღვრის დომენი. ყველა მნიშვნელობა, რომელსაც იღებს დამოკიდებული ცვლადი (ცვლადი წ), ჩამოაყალიბეთ ფუნქციის მნიშვნელობების დიაპაზონი.

ფუნქციის გრაფიკიმოვუწოდებთ კოორდინატთა სიბრტყის ყველა წერტილის სიმრავლეს, რომელთა აბსციები უდრის არგუმენტის მნიშვნელობებს, ხოლო ორდინატები ტოლია ფუნქციის შესაბამისი მნიშვნელობების, ანუ მნიშვნელობების. ცვლადი გამოსახულია აბსცისის ღერძის გასწვრივ xდა ცვლადის მნიშვნელობები გამოსახულია ორდინატთა ღერძის გასწვრივ წ. ფუნქციის გრაფიკისთვის, თქვენ უნდა იცოდეთ ფუნქციის თვისებები. ფუნქციის ძირითადი თვისებები ქვემოთ იქნება განხილული!

ფუნქციის გრაფიკის შესაქმნელად, ჩვენ გირჩევთ გამოიყენოთ ჩვენი პროგრამა - გრაფიკული ფუნქციები ონლაინ. თუ თქვენ გაქვთ რაიმე შეკითხვები ამ გვერდის მასალის შესწავლისას, ყოველთვის შეგიძლიათ დასვათ ისინი ჩვენს ფორუმზე. ასევე ფორუმზე დაგეხმარებიან ამოცანების გადაჭრაში მათემატიკაში, ქიმიაში, გეომეტრიაში, ალბათობის თეორიაში და სხვა ბევრ საგანში!

ფუნქციების ძირითადი თვისებები.

1) ფუნქციის დომენი და ფუნქციის დიაპაზონი.

ფუნქციის დომენი არის ყველა მოქმედი არგუმენტის მნიშვნელობების ნაკრები x(ცვლადი x), რისთვისაც ფუნქცია y = f(x)განსაზღვრული.
ფუნქციის დიაპაზონი არის ყველა რეალური მნიშვნელობის სიმრავლე წ, რომელსაც ფუნქცია იღებს.

ელემენტარულ მათემატიკაში ფუნქციებს სწავლობენ მხოლოდ ნამდვილ რიცხვთა სიმრავლეზე.

2) ფუნქცია ნულები.

ფუნქცია ნული არის არგუმენტის მნიშვნელობა, რომლის დროსაც ფუნქციის მნიშვნელობა ნულის ტოლია.

3) ფუნქციის მუდმივი ნიშნის ინტერვალები.

ფუნქციის მუდმივი ნიშნის ინტერვალები არის არგუმენტების მნიშვნელობების ნაკრები, რომლებზეც ფუნქციის მნიშვნელობები მხოლოდ დადებითი ან მხოლოდ უარყოფითია.

4) ფუნქციის ერთფეროვნება.

მზარდი ფუნქცია (გარკვეულ ინტერვალში) არის ფუნქცია, რომელშიც არგუმენტის უფრო დიდი მნიშვნელობა ამ ინტერვალიდან შეესაბამება ფუნქციის უფრო დიდ მნიშვნელობას.

კლებადი ფუნქცია (გარკვეულ ინტერვალში) არის ფუნქცია, რომელშიც არგუმენტის უფრო დიდი მნიშვნელობა ამ ინტერვალიდან შეესაბამება ფუნქციის უფრო მცირე მნიშვნელობას.

5) ლუწი (კენტი) ფუნქცია.

ლუწი ფუნქცია არის ფუნქცია, რომლის განსაზღვრის დომენი სიმეტრიულია წარმოშობის და ნებისმიერის მიმართ Xგანმარტების სფეროდან თანასწორობა f(-x) = f(x). ლუწი ფუნქციის გრაფიკი სიმეტრიულია ორდინატთან მიმართებაში.

უცნაური ფუნქცია არის ფუნქცია, რომლის განსაზღვრის დომენი სიმეტრიულია წარმოშობის მიმართ და ნებისმიერისთვის Xგანმარტების სფეროდან თანასწორობა მართალია f(-x) = - f(x). კენტი ფუნქციის გრაფიკი სიმეტრიულია წარმოშობის მიმართ.

6) შეზღუდული და შეუზღუდავი ფუნქციები.

ფუნქციას უწოდებენ შეზღუდულს, თუ არის დადებითი რიცხვი M ისეთი, რომ |f(x)| ≤ M x-ის ყველა მნიშვნელობისთვის. თუ ასეთი რიცხვი არ არსებობს, მაშინ ფუნქცია შეუზღუდავია.

7) ფუნქციის პერიოდულობა.

ფუნქცია f(x) პერიოდულია, თუ არსებობს არა ნულოვანი რიცხვი T ისეთი, რომ ნებისმიერი x-ისთვის f(x+T) = f(x). ამ უმცირეს რიცხვს ეწოდება ფუნქციის პერიოდი. ყველა ტრიგონომეტრიული ფუნქცია პერიოდულია. (ტრიგონომეტრიული ფორმულები).

ფუნქციის ამ თვისებების შესწავლის შემდეგ, თქვენ შეგიძლიათ მარტივად შეისწავლოთ ფუნქცია და, ფუნქციის თვისებების გამოყენებით, შეგიძლიათ შექმნათ ფუნქციის გრაფიკი. ასევე გადახედეთ მასალას სიმართლის ცხრილის, გამრავლების ცხრილის, პერიოდული ცხრილის, წარმოებულების ცხრილისა და ინტეგრალების ცხრილის შესახებ.

ფუნქცია ნულები

რა არის ფუნქციის ნულები? როგორ განვსაზღვროთ ფუნქციის ნულები ანალიტიკურად და გრაფიკულად?

ფუნქცია ნულები- ეს არის არგუმენტის მნიშვნელობები, რომლებშიც ფუნქცია ნულის ტოლია.

y=f(x) ფორმულით მოცემული ფუნქციის ნულების საპოვნელად უნდა ამოხსნათ განტოლება f(x)=0.

თუ განტოლებას არ აქვს ფესვები, ფუნქციას არ აქვს ნულები.

1) იპოვეთ y=3x+15 წრფივი ფუნქციის ნულები.

ფუნქციის ნულების საპოვნელად ამოხსენით განტოლება 3x+15 =0.

ამრიგად, ფუნქციის ნული არის y=3x+15 - x= -5.

2) იპოვეთ f(x)=x²-7x+12 კვადრატული ფუნქციის ნულები.

ფუნქციის ნულების საპოვნელად ამოხსენით კვადრატული განტოლება

მისი ფესვები x1=3 და x2=4 ამ ფუნქციის ნულებია.

3) იპოვეთ ფუნქციის ნულები

წილადს აქვს აზრი, თუ მნიშვნელი არ არის ნულოვანი. ამიტომ, x²-1≠0, x² ≠ 1, x ≠±1. ანუ მოცემული ფუნქციის განსაზღვრის დომენი (DO)

განტოლების ფესვებიდან x²+5x+4=0 x1=-1 x2=-4 მხოლოდ x=-4 შედის განმარტების დომენში.

გრაფიკულად მოცემული ფუნქციის ნულების საპოვნელად, თქვენ უნდა იპოვოთ ფუნქციის გრაფიკის გადაკვეთის წერტილები აბსცისის ღერძთან.

თუ გრაფიკი არ კვეთს Ox-ღერძს, ფუნქციას არ აქვს ნულები.

ფუნქციას, რომლის გრაფიკი ნაჩვენებია სურათზე, აქვს ოთხი ნული -

ალგებრაში ფუნქციის ნულების პოვნის პრობლემა ჩნდება როგორც დამოუკიდებელი ამოცანის სახით, ასევე სხვა ამოცანების ამოხსნისას, მაგალითად, ფუნქციის შესწავლისას, უტოლობების ამოხსნისას და ა.შ.

www.algebraclass.ru

ფუნქციის ნულოვანი წესი

ფუნქციების ძირითადი ცნებები და თვისებები

წესი მიმოწერის (კანონი). მონოტონური ფუნქცია .

შეზღუდული და შეუზღუდავი ფუნქციები. უწყვეტი და

უწყვეტი ფუნქციები . ლუწი და კენტი ფუნქციები.

პერიოდული ფუნქცია. ფუნქციის პერიოდი.

ფუნქცია ნულები . ასიმპტოტი .

განსაზღვრების დომენი და ფუნქციის მნიშვნელობების დიაპაზონი. ელემენტარულ მათემატიკაში ფუნქციებს სწავლობენ მხოლოდ ნამდვილ რიცხვთა სიმრავლეზე რ . ეს ნიშნავს, რომ ფუნქციის არგუმენტს შეუძლია მიიღოს მხოლოდ ის რეალური მნიშვნელობები, რომლებისთვისაც არის განსაზღვრული ფუნქცია, ე.ი. ის ასევე იღებს მხოლოდ რეალურ ღირებულებებს. Რამოდენიმე X ყველა მოქმედი არგუმენტის მნიშვნელობა x, რისთვისაც ფუნქცია წ = ვ (x) არის განსაზღვრული, ე.წ ფუნქციის დომენი. Რამოდენიმე ი ყველა რეალური ღირებულება წ, რომელსაც ფუნქცია იღებს, ეწოდება ფუნქციის დიაპაზონი. ახლა ჩვენ შეგვიძლია მივცეთ ფუნქციის უფრო ზუსტი განმარტება: წესი სიმრავლეს შორის შესაბამისობის (კანონი). Xდა ი , რომლის მიხედვითაც სიმრავლიდან თითოეული ელემენტისთვის Xთქვენ შეგიძლიათ იპოვოთ ერთი და მხოლოდ ერთი ელემენტი ნაკრებიდან ი, ფუნქციას უწოდებენ .

ამ განმარტებიდან გამომდინარეობს, რომ ფუნქცია განიხილება განსაზღვრულად, თუ:

— მითითებულია ფუნქციის განსაზღვრის დომენი X ;

— მითითებულია ფუნქციის დიაპაზონი ი ;

— მიმოწერის წესი (კანონი) ცნობილია და ისეთი, რომ თითოეული

არგუმენტის მნიშვნელობა, მხოლოდ ერთი ფუნქციის მნიშვნელობის პოვნაა შესაძლებელი.

ფუნქციის უნიკალურობის ეს მოთხოვნა სავალდებულოა.

მონოტონური ფუნქცია. თუ არგუმენტის რომელიმე ორი მნიშვნელობისთვის x 1 და x 2 მდგომარეობა x 2 > x 1 მოყვება ვ (x 2) > ვ (x 1), შემდეგ ფუნქცია ვ (x) ეწოდება იზრდება; თუ რომელიმესთვის x 1 და x 2 მდგომარეობა x 2 > x 1 მოყვება ვ (x 2)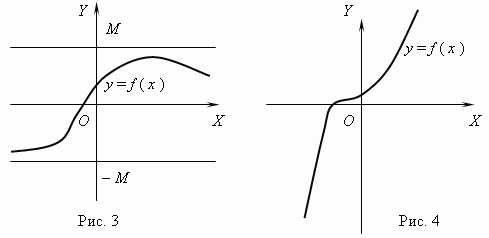

3-ზე ნაჩვენები ფუნქცია შეზღუდულია, მაგრამ არა მონოტონური. 4-ში მოცემული ფუნქცია არის საპირისპირო, მონოტონური, მაგრამ შეუზღუდავი. (განმარტეთ ეს გთხოვთ!).

უწყვეტი და უწყვეტი ფუნქციები. ფუნქცია წ = ვ (x) ეწოდება უწყვეტი წერტილში x = ა, თუ:

1) ფუნქცია განისაზღვრება, როდესაც x = ა, ე.ი. ვ (ა) არსებობს;

2) არსებობს სასრულილიმიტის ლიმიტი ვ (x) ;

თუ ამ პირობებიდან ერთი მაინც არ არის დაკმაყოფილებული, მაშინ ფუნქცია გამოიძახება ასაფეთქებელიწერტილში x = ა .

თუ ფუნქცია უწყვეტია დროს ყველას მისი განმარტების სფეროს წერტილები, მაშინ ე.წ უწყვეტი ფუნქცია.

ლუწი და კენტი ფუნქციები. თუ ამისთვის ნებისმიერი xფუნქციის განსაზღვრის დომენიდან მოქმედებს შემდეგი: ვ (— x) = ვ (x), შემდეგ ფუნქცია გამოიძახება თუნდაც; თუ ეს მოხდება: ვ (— x) = — ვ (x), შემდეგ ფუნქცია გამოიძახება უცნაური. ლუწი ფუნქციის გრაფიკი სიმეტრიული Y ღერძის მიმართ(სურ. 5), კენტი ფუნქციის გრაფიკი სიმ მეტრიკა წარმოშობის მიმართ(ნახ. 6).

პერიოდული ფუნქცია. ფუნქცია ვ (x) — პერიოდული, თუ ასეთი რამ არსებობს არანულოვანინომერი თრისთვის ნებისმიერი xფუნქციის განსაზღვრის დომენიდან მოქმედებს შემდეგი: ვ (x + თ) = ვ (x). ეს სულ მცირენომერს ეძახიან ფუნქციის პერიოდი. ყველა ტრიგონომეტრიული ფუნქცია პერიოდულია.

მაგალითი 1. დაამტკიცე ეს ცოდვა xაქვს 2 პერიოდი.

გამოსავალი: ჩვენ ვიცით, რომ ცოდვა ( x+ 2 ნ) = ცოდვა x, სად ნ= 0, ± 1, ± 2, ...

ამიტომ, დამატება 2 ნარა სინუს არგუმენტამდე

ცვლის მის მნიშვნელობას ე. არის სხვა ნომერი ამით?

მოდი ვიჩვენოთ, რომ პ– ასეთი რიცხვი, ე.ი. თანასწორობა:

მოქმედებს ნებისმიერი ღირებულებისთვის x. მაგრამ შემდეგ აქვს

ადგილზე და x= / 2, ე.ი.

sin(/2 + პ) = ცოდვა / 2 = 1.

მაგრამ შემცირების ფორმულის მიხედვით sin (/ 2 + პ) = cos პ. მერე

ბოლო ორი ტოლობიდან გამომდინარეობს, რომ cos პ= 1, მაგრამ ჩვენ

ჩვენ ვიცით, რომ ეს მართალია მხოლოდ მაშინ, როდესაც პ = 2 ნ. ვინაიდან ყველაზე პატარა

არანულოვანი რიცხვი 2-დან ნარის 2, მაშინ ეს რიცხვი

და არის პერიოდი ცოდვა x. ანალოგიურად შეიძლება დადასტურდეს, რომ 2

ასევე პერიოდია cos x .

დაამტკიცეთ, რომ ფუნქციები გარუჯულია xდა საწოლი xაქვს პერიოდი.

მაგალითი 2. რა რიცხვია sin 2 ფუნქციის პერიოდი x ?

გამოსავალი: განვიხილოთ ცოდვა 2 x= ცოდვა (2 x+ 2 ნ) = ცოდვა [ 2 ( x + ნ) ] .

ჩვენ ვხედავთ, რომ დაემატება ნკამათს x, არ იცვლება

ფუნქციის მნიშვნელობა. ყველაზე პატარა არა ნულოვანი რიცხვი

საწყისი ნარის , ასე რომ, ეს არის ცოდვის 2 პერიოდი x .

ფუნქცია ნულები. არგუმენტის მნიშვნელობა, რომლის დროსაც ფუნქცია 0-ის ტოლია, გამოძახებულია ნული ( root) ფუნქცია. ფუნქციას შეიძლება ჰქონდეს რამდენიმე ნული. მაგალითად, ფუნქცია წ = x (x + 1) (x- 3) აქვს სამი ნული: x = 0, x = — 1, x= 3. გეომეტრიულად null ფუნქცია – ეს არის ფუნქციის გრაფიკის ღერძთან გადაკვეთის წერტილის აბსცისა X .

ნახაზი 7 გვიჩვენებს ფუნქციის გრაფიკს ნულებით: x = ა , x = ბდა x = გ .

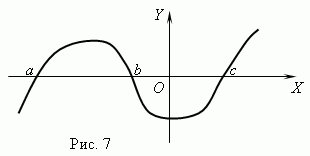
ასიმპტოტი. თუ ფუნქციის გრაფიკი განუსაზღვრელი ვადით უახლოვდება გარკვეულ ხაზს, როდესაც ის საწყისს შორდება, მაშინ ამ წრფეს ე.წ. ასიმპტოტი.

თემა 6. „ინტერვალის მეთოდი“.

თუ f (x) f (x 0) x x 0-ისთვის, მაშინ გამოიძახება ფუნქცია f (x). უწყვეტი x0 წერტილში.

თუ ფუნქცია უწყვეტია I რაღაც ინტერვალის ყველა წერტილში, მაშინ მას უწოდებენ უწყვეტი ინტერვალზემე (ინტერვალი I ეწოდება ფუნქციის უწყვეტობის ინტერვალი). ამ ინტერვალზე ფუნქციის გრაფიკი არის უწყვეტი ხაზი, რომელიც, მათი თქმით, შეიძლება „დაიხატოს ფანქრის აწევის გარეშე“.

უწყვეტი ფუნქციების თვისება.

თუ ინტერვალზე (a ; b) ფუნქცია f უწყვეტია და არ ქრება, მაშინ ის ინარჩუნებს მუდმივ ნიშანს ამ ინტერვალზე.

ამ თვისებას ეფუძნება უტოლობების ერთი ცვლადით ამოხსნის მეთოდი, ინტერვალის მეთოდი. დაე, ფუნქცია f(x) იყოს უწყვეტი I ინტერვალზე და ქრება ამ ინტერვალის წერტილების სასრულ რაოდენობაზე. უწყვეტი ფუნქციების თვისებით ეს წერტილები I იყოფა ინტერვალებად, რომელთაგან თითოეულში უწყვეტი ფუნქცია f(x) c ინარჩუნებს მუდმივ ნიშანს. ამ ნიშნის დასადგენად საკმარისია გამოვთვალოთ f(x) ფუნქციის მნიშვნელობა ყოველი ასეთი ინტერვალიდან ნებისმიერ წერტილში. ამის საფუძველზე ვიღებთ უტოლობების ამოხსნის შემდეგ ალგორითმს ინტერვალის მეთოდით.

ფორმის უტოლობების ინტერვალის მეთოდი

იპოვეთ f(x) ფუნქციის განსაზღვრის დომენი;

იპოვეთ f(x) ფუნქციის ნულები;

დახაზეთ ფუნქციის განსაზღვრის დომენი და ნულები რიცხვით წრფეზე. ფუნქციის ნულები ყოფს მის განსაზღვრების დომენს ინტერვალებად, რომელთაგან თითოეულში ფუნქცია ინარჩუნებს მუდმივ ნიშანს;

იპოვეთ ფუნქციის ნიშნები მიღებულ ინტერვალებში ფუნქციის მნიშვნელობის გამოთვლით ყოველი ინტერვალიდან რომელიმე წერტილში;

დაწერე პასუხი.

ინტერვალის მეთოდი. საშუალო დონე.

გსურთ გამოსცადოთ თქვენი ძალა და გაიგოთ შედეგი, რამდენად მზად ხართ ერთიანი სახელმწიფო გამოცდისთვის ან ერთიანი სახელმწიფო გამოცდისთვის?

ხაზოვანი ფუნქცია

ფორმის ფუნქციას წრფივი ეწოდება. მაგალითად ავიღოთ ფუნქცია. ის დადებითია 3″>-ზე და უარყოფითია. წერტილი არის ფუნქციის ნული (). მოდით ვაჩვენოთ ამ ფუნქციის ნიშნები რიცხვის ღერძზე:

ჩვენ ვამბობთ, რომ "ფუნქცია ცვლის ნიშანს წერტილის გავლისას".

ჩანს, რომ ფუნქციის ნიშნები შეესაბამება ფუნქციის გრაფიკის პოზიციას: თუ გრაფიკი ღერძის ზემოთ არის, ნიშანი არის “ ”, თუ მის ქვემოთ არის “ ”.

თუ მიღებულ წესს განვაზოგადებთ თვითნებურ წრფივ ფუნქციაზე, მივიღებთ შემდეგ ალგორითმს:

ფუნქციის ნულის პოვნა;

ჩვენ აღვნიშნავთ მას რიცხვით ღერძზე;

ჩვენ განვსაზღვრავთ ფუნქციის ნიშანს ნულის მოპირდაპირე მხარეს.

კვადრატული ფუნქცია

იმედია გახსოვთ როგორ ამოხსნათ კვადრატული უტოლობა? თუ არა, წაიკითხეთ თემა "კვადრატული უტოლობა". შეგახსენებთ კვადრატული ფუნქციის ზოგად ფორმას: .

ახლა გავიხსენოთ რა ნიშნები აქვს კვადრატულ ფუნქციას. მისი გრაფიკი არის პარაბოლა და ფუნქცია იღებს ნიშანს " " მათთვის, რომლებშიც პარაბოლა ღერძის ზემოთ არის და " " - თუ პარაბოლა ღერძის ქვემოთაა:

თუ ფუნქციას აქვს ნულები (მნიშვნელობები, რომლებშიც), პარაბოლა კვეთს ღერძს ორ წერტილში - შესაბამისი კვადრატული განტოლების ფესვები. ამრიგად, ღერძი იყოფა სამ ინტერვალად და ფუნქციის ნიშნები მონაცვლეობით იცვლება თითოეულ ფესვზე გავლისას.

შესაძლებელია თუ არა ნიშნების დადგენა ყოველ ჯერზე პარაბოლის დახატვის გარეშე?

შეგახსენებთ, რომ კვადრატული ტრინომი შეიძლება იყოს ფაქტორიზირებული:

მოდით აღვნიშნოთ ფესვები ღერძზე:

ჩვენ გვახსოვს, რომ ფუნქციის ნიშანი შეიძლება შეიცვალოს მხოლოდ ფესვში გავლისას. გამოვიყენოთ ეს ფაქტი: თითოეული სამი ინტერვალისთვის, რომლებშიც ღერძი იყოფა ფესვებით, საკმარისია ფუნქციის ნიშანი მხოლოდ ერთ თვითნებურად არჩეულ წერტილში განვსაზღვროთ: ინტერვალის დანარჩენ წერტილებში ნიშანი იგივე იქნება. .

ჩვენს მაგალითში: 3″>-ზე ორივე გამონათქვამი ფრჩხილებში დადებითია (ჩანაცვლება, მაგალითად: 0″>). ღერძზე ვსვამთ ნიშანს:

კარგად, როდესაც (შემცვლელი, მაგალითად), ორივე ფრჩხილი უარყოფითია, რაც ნიშნავს, რომ პროდუქტი დადებითია:

სწორედ ეს არის ინტერვალის მეთოდი: ფაქტორების ნიშნების ცოდნა თითოეულ ინტერვალზე, ჩვენ განვსაზღვრავთ მთელი პროდუქტის ნიშანს.

ასევე განვიხილოთ შემთხვევები, როდესაც ფუნქციას არ აქვს ნულები, ან მხოლოდ ერთი.

თუ ისინი იქ არ არიან, მაშინ ფესვები არ არსებობს. ეს ნიშნავს, რომ არ იქნება "ძირში გავლა". ეს ნიშნავს, რომ ფუნქცია იღებს მხოლოდ ერთ ნიშანს მთელ რიცხვით ხაზზე. მისი მარტივად დადგენა შესაძლებელია ფუნქციაში ჩანაცვლებით.

თუ მხოლოდ ერთი ფესვია, პარაბოლა ეხება ღერძს, ამიტომ ფუნქციის ნიშანი ფესვში გავლისას არ იცვლება. რა წესი შეიძლება გამოვიყენოთ ასეთ სიტუაციებში?

თუ ასეთ ფუნქციას აფასებთ, მიიღებთ ორ იდენტურ ფაქტორს:

და ნებისმიერი კვადრატული გამოხატულება არის არაუარყოფითი! ამიტომ, ფუნქციის ნიშანი არ იცვლება. ასეთ შემთხვევებში გამოვყოფთ ფესვს, რომლის გავლისას ნიშანი არ იცვლება, კვადრატით შემოხაზვით:

ასეთ ფესვს დავარქმევთ მრავლობითი.

ინტერვალის მეთოდი უტოლობებში

ახლა ნებისმიერი კვადრატული უტოლობა შეიძლება ამოიხსნას პარაბოლის დახატვის გარეშე. საკმარისია მხოლოდ კვადრატული ფუნქციის ნიშნების ღერძზე განთავსება და უტოლობის ნიშნის მიხედვით ინტერვალების შერჩევა. Მაგალითად:

მოდით გავზომოთ ფესვები ღერძზე და მოვათავსოთ ნიშნები:

ჩვენ გვჭირდება ღერძის ნაწილი " " ნიშნით; ვინაიდან უთანასწორობა არ არის მკაცრი, თავად ფესვებიც შედის ამოხსნაში:

ახლა განვიხილოთ რაციონალური უტოლობა - უტოლობა, რომლის ორივე მხარე რაციონალური გამონათქვამებია (იხ. „რაციონალური განტოლებები“).

მაგალითი:

ყველა ფაქტორი, გარდა ერთისა, აქ არის „წრფივი“, ანუ ისინი შეიცავს ცვლადს მხოლოდ პირველ ხარისხზე. ასეთი წრფივი ფაქტორები გვჭირდება ინტერვალის მეთოდის გამოსაყენებლად - ნიშანი იცვლება მათ ფესვებში გავლისას. მაგრამ მულტიპლიკატორს საერთოდ არ აქვს ფესვები. ეს ნიშნავს, რომ ის ყოველთვის პოზიტიურია (შეამოწმეთ ეს თქვენთვის) და, შესაბამისად, არ იმოქმედებს მთელი უთანასწორობის ნიშანზე. ეს ნიშნავს, რომ ჩვენ შეგვიძლია გავყოთ უტოლობის მარცხენა და მარჯვენა მხარეები მასზე და ამით მოვიშოროთ იგი:

ახლა ყველაფერი იგივეა, რაც იყო კვადრატული უტოლობების დროს: ჩვენ განვსაზღვრავთ რა წერტილებში ხდება თითოეული ფაქტორი ნული, აღვნიშნავთ ამ წერტილებს ღერძზე და ვაწყობთ ნიშნებს. მინდა თქვენი ყურადღება გავამახვილო ძალიან მნიშვნელოვან ფაქტზე:

ლუწი რიცხვის შემთხვევაში ვაკეთებთ ისევე, როგორც ადრე: წერტილს ვახვევთ კვადრატს და ფესვზე გავლისას არ ვცვლით ნიშანს. მაგრამ კენტი რიცხვის შემთხვევაში ეს წესი არ მოქმედებს: ნიშანი მაინც შეიცვლება ფესვზე გავლისას. მაშასადამე, ისეთ ძირთან დამატებით არაფერს ვაკეთებთ, თითქოს მრავლობითი არ იყოს. ზემოაღნიშნული წესები ვრცელდება ყველა ლუწ და კენტ ძალაზე.

რა უნდა ჩავწეროთ პასუხში?

თუ ნიშნების მონაცვლეობა ირღვევა, ძალიან ფრთხილად უნდა იყოთ, რადგან თუ უთანასწორობა მკაცრი არ არის, პასუხი უნდა შეიცავდეს ყველა დაჩრდილული წერტილი. მაგრამ ზოგიერთი მათგანი ხშირად ცალ-ცალკე დგას, ანუ ისინი არ შედის დაჩრდილულ ზონაში. ამ შემთხვევაში, ჩვენ მათ ვუმატებთ პასუხს, როგორც იზოლირებულ წერტილებს (ხუჭუჭა ბრეკეტებში):

მაგალითები (გადაწყვიტეთ თქვენთვის):

პასუხები:

1. თუ ფაქტორებს შორის ის მარტივია, ეს არის ფესვი, რადგან ის შეიძლება წარმოდგენილი იყოს როგორც.
   .

არგუმენტის მნიშვნელობები ზ რომელიც ვ(ზ) მიდის ნულამდე მოწოდებული. ნულოვანი წერტილი, ე.ი. თუ ვ(ა) = 0, მაშინ ა - ნულოვანი წერტილი.

დეფ.Წერტილი ადაურეკა ნულოვანი შეკვეთან , თუ FKP შეიძლება წარმოდგენილი იყოს ფორმით ვ(ზ) = , სად
ანალიტიკური ფუნქცია და
0.

ამ შემთხვევაში, ტეილორის სერიის ფუნქციის გაფართოება (43), პირველი ნ კოეფიციენტები ნულის ტოლია

= =

და ა.შ. დაადგინეთ ნულის რიგი
და (1 – cos ზ) ზე ზ = 0

=
=

ნულოვანი 1-ლი რიგი

1 – კოზ ზ =
=

ნულოვანი მე-2 რიგი

დეფ.Წერტილი ზ =
დაურეკა წერტილი უსასრულობაზედა ნულიფუნქციები ვ(ზ), თუ ვ(
) = 0. ასეთი ფუნქცია შეიძლება გაფართოვდეს სერიებად უარყოფითი ხარისხებით ზ : ვ(ზ) =
. თუ პირველი ნ კოეფიციენტები ნულის ტოლია, მაშინ მივდივართ ნულოვანი შეკვეთა ნ უსასრულობის წერტილში: ვ(ზ) = ზ - ნ
.

ცალკეული სინგულარული წერტილები იყოფა: ა) მოსახსნელი სინგულარული წერტილები; ბ) წესრიგის ბოძებინ; V) არსებითად ცალკეული წერტილები.

Წერტილი ადაურეკა მოსახსნელი სინგულარული წერტილიფუნქციები ვ(ზ) თუ ზე ზ
ა ლიმი ვ(ზ) = თან -საბოლოო ნომერი .

Წერტილი ადაურეკა წესრიგის პოლუსინ (ნ 1) ფუნქციები ვ(ზ), თუ შებრუნებული ფუნქცია
= 1/ ვ(ზ) აქვს ნულოვანი რიგი ნწერტილში ა.ასეთი ფუნქცია ყოველთვის შეიძლება წარმოდგენილი იყოს როგორც ვ(ზ) =
, სად
- ანალიტიკური ფუნქცია და
.

Წერტილი ადაურეკა არსებითად განსაკუთრებული წერტილიფუნქციები ვ(ზ), თუ ზე ზ
ა ლიმი ვ(ზ) არ არსებობს.

ლორანის სერია

განვიხილოთ რგოლის კონვერგენციის რეგიონის შემთხვევა რ < | ზ 0 – ა| < რწერტილზე ორიენტირებული აფუნქციისთვის ვ(ზ). წარმოგიდგინოთ ორი ახალი წრე ლ 1 (რ) და ლ 2 (რ) წერტილით რგოლის საზღვრებთან ზ 0 მათ შორის. მოდით გავაკეთოთ რგოლის ჭრილი, დავაკავშიროთ წრეები ჭრილის კიდეების გასწვრივ, გადავიდეთ უბრალოდ დაკავშირებულ რეგიონზე და

ქოშის ინტეგრალური ფორმულა (39) ვიღებთ ორ ინტეგრალს z ცვლადზე

ვ(ზ 0) =
+
, (42)

სადაც ინტეგრაცია საპირისპირო მიმართულებით მიდის.

ინტეგრალური ზედ ლშესრულებულია 1 პირობა | ზ 0 – ა | > | ზ – ა |, და ინტეგრალური ზედ ლ 2 შებრუნებული მდგომარეობა | ზ 0 – ა | < | ზ – ა |. ამიტომ, ფაქტორი 1/( ზ – ზ 0) გაფართოვდეს სერიებად (a) ინტეგრალურ ზედ ლ 2 და სერიებში (b) ინტეგრალურ ზედ ლ 1 . შედეგად, ჩვენ ვიღებთ გაფართოებას ვ(ზ) რგოლის არეში in ლორანის სერიადადებითი და უარყოფითი ძალებით ( ზ 0 – ა)

ვ(ზ 0) =
ა ნ (ზ 0 -ა) ნ (43)

სად ა ნ =
=
;ა -ნ =

პოზიტიური ძალების გაფართოება (ზ 0 - ა) დაუძახა მარჯვენა ნაწილი Laurent სერია (ტეილორის სერია) და გაფართოება ნეგატიურ ძალებში ჰქვია. მთავარი ნაწილილორანის სერია.

თუ წრის შიგნით ლ 1 არ არის სინგულარული წერტილები და ფუნქცია ანალიტიკურია, მაშინ (44)-ში პირველი ინტეგრალი ტოლია ნულის კოშის თეორემით და მხოლოდ სწორი ნაწილი რჩება ფუნქციის გაფართოებაში. გაფართოებაში (45) უარყოფითი ძალა ჩნდება მხოლოდ მაშინ, როდესაც ანალიტიკურობა ირღვევა შიდა წრეში და ემსახურება ფუნქციის აღწერას იზოლირებულ სინგულურ წერტილებთან.

ლორანის სერიის (45) ასაგებად ვ(ზ) შეგიძლიათ გამოთვალოთ გაფართოების კოეფიციენტები ზოგადი ფორმულის გამოყენებით ან გამოიყენოთ ელემენტარული ფუნქციების გაფართოებები, რომლებიც შედის ვ(ზ).

ტერმინების რაოდენობა ( ნ) ლორანის სერიის ძირითადი ნაწილი დამოკიდებულია სინგულარული წერტილის ტიპზე: მოსახსნელი სინგულარული წერტილი (ნ = 0) ; არსებითად ცალკეული წერტილი (ნ
); ბოძინ- ვაა შეკვეთა(ნ - საბოლოო ნომერი).

და ამისთვის ვ(ზ) = წერტილი ზ = 0 მოსახსნელი სინგულარული წერტილი,რადგან ძირითადი ნაწილი არ არის. ვ(ზ) = (ზ -
) = 1 -

ბ) ამისთვის ვ(ზ) = წერტილი ზ = 0 - 1-ლი რიგის ბოძი

ვ(ზ) = (ზ -
) = -

გ) ამისთვის ვ(ზ) = ე 1 / ზწერტილი ზ = 0 - არსებითად ცალკეული წერტილი

ვ(ზ) = ე 1 / ზ =

თუ ვ(ზ) არის ანალიტიკური დომენში დგარდა იმისა მიზოლირებული სინგულარული წერტილები და | ზ 1 | < |ზ 2 | < . . . < |ზ მ| , მაშინ ძალაუფლებაში ფუნქციის გაფართოებისას ზმთელი თვითმფრინავი იყოფა მ+ 1 ბეჭედი | ზ მე | < | ზ | < | ზ მე+ 1 | და Laurent სერიას აქვს განსხვავებული გარეგნობა თითოეული ბეჭდისთვის. ძალაუფლების გაფართოებისას ( ზ – ზ მე ) ლორანის სერიის კონვერგენციის რეგიონია წრე | ზ – ზ მე | < რ, სად რ - მანძილი უახლოეს ცალკეულ წერტილამდე.

და ა.შ. მოდით გავაფართოვოთ ფუნქცია ვ(ზ) =Laurent-ის სერიაში ძალაუფლებაში ზდა ( ზ - 1).

გამოსავალი. გამოვსახოთ ფუნქცია ფორმაში ვ(ზ) = - ზ 2 . ჩვენ ვიყენებთ გეომეტრიული პროგრესიის ჯამის ფორმულას
. წრეში |z|< 1 ряд сходится и ვ(ზ) = - ზ 2 (1 + ზ + ზ 2 + ზ 3 + ზ 4 + . . .) = - ზ 2 - ზ 3 - ზ 4 - . . . , ე.ი. დაშლა შეიცავს მხოლოდ სწორინაწილი. გადავიდეთ წრის გარე რეგიონში |z| > 1. გამოვსახოთ ფუნქცია ფორმაში
, სადაც 1/| ზ| < 1, и получим разложение ვ(ზ) = ზ
=ზ + 1 +

იმიტომ რომ , ფუნქციის გაფართოება უფლებამოსილებაში ( ზ - 1) ჰგავს ვ(ზ) = (ზ - 1) -1 + 2 + (ზ - 1) ყველასთვის
1.

და ა.შ. გააფართოვეთ ფუნქცია Laurent სერიაში ვ(ზ) =
: ა) გრადუსით ზწრეში | ზ| < 1; b) по степеням ზ ბეჭედი 1< |ზ| < 3 ; c) по степеням (ზ – 2).ხსნარი. დავშალოთ ფუნქცია მარტივ წილადებად
= =+=
. პირობებიდან ზ =1
ა = -1/2 , ზ =3
ბ = ½.

ა) ვ(ზ) = ½ [
] = ½ [
-(1/3)
], | ზ|< 1.

ბ) ვ(ზ) = - ½ [
+
] = - (
), 1-ზე< |ზ| < 3.

თან) ვ(ზ) = ½ [
]= - ½ [
] =

= - ½ = -
, ერთად |2 - ზ| < 1

ეს არის 1 რადიუსის წრე, რომლის ცენტრია ზ = 2 .

ზოგიერთ შემთხვევაში, სიმძლავრის სერია შეიძლება შემცირდეს გეომეტრიულ პროგრესირებამდე და ამის შემდეგ ადვილია მათი კონვერგენციის რეგიონის დადგენა.

და ა.შ. გამოიკვლიეთ სერიის კონვერგენცია

. . . + + + + 1 + () + () 2 + () 3 + . . .

გამოსავალი. ეს არის ორი გეომეტრიული პროგრესიის ჯამი ქ 1 = , ქ 2 = () . მათი დაახლოების პირობებიდან გამომდინარეობს < 1 , < 1 или |ზ| > 1 , |ზ| < 2 , т.е. область сходимости ряда кольцо 1 < |ზ| < 2 .

2. ვიპოვოთ ფუნქციის ნულები.

f(x) x-ზე .

უპასუხეთ f(x) x-ზე .

2) x 2 >-4x-5;

x 2 +4x +5>0;

დავუშვათ f(x)=x 2 +4x +5, შემდეგ ვიპოვოთ x, რომლისთვისაც f(x)>0,

D=-4 ნულები არ არის.

4. უტოლობათა სისტემები. უტოლობა და უტოლობათა სისტემები ორი ცვლადით

1) უტოლობათა სისტემის ამონახსნების სიმრავლე არის მასში შემავალი უტოლობების ამონახსნების სიმრავლეების კვეთა.

2) f(x;y)>0 უტოლობის ამონახსნების სიმრავლე შეიძლება გრაფიკულად იყოს გამოსახული კოორდინატულ სიბრტყეზე. როგორც წესი, f(x;y) = 0 განტოლებით განსაზღვრული წრფე სიბრტყეს ყოფს 2 ნაწილად, რომელთაგან ერთი არის უტოლობის ამოხსნა. იმის დასადგენად, თუ რომელი ნაწილი, თქვენ უნდა ჩაანაცვლოთ თვითნებური წერტილის კოორდინატები M(x0;y0), რომელიც არ დევს f(x;y)=0 წრფეზე უტოლობაში. თუ f(x0;y0) > 0, მაშინ უტოლობის ამონახსნი არის M0 წერტილის შემცველი სიბრტყის ნაწილი. თუ f(x0;y0)<0, то другая часть плоскости.

3) უტოლობათა სისტემის ამონახსნების სიმრავლე არის მასში შემავალი უტოლობების ამონახსნების სიმრავლეების კვეთა. მოდით, მაგალითად, მივცეთ უტოლობათა სისტემა:

.

პირველი უტოლობისთვის ამონახსნთა სიმრავლე არის წრე 2 რადიუსით და ცენტრით საწყისზე, ხოლო მეორესთვის ეს არის ნახევრად სიბრტყე, რომელიც მდებარეობს სწორი ხაზის ზემოთ 2x+3y=0. ამ სისტემის ამონახსნების სიმრავლე არის ამ სიმრავლეთა კვეთა, ე.ი. ნახევარწრიული.

4) მაგალითი. ამოხსენით უტოლობების სისტემა:

1-ლი უტოლობის ამონახსნი არის სიმრავლე, მე-2 არის სიმრავლე (2;7) და მესამე არის სიმრავლე.

ამ სიმრავლეთა კვეთა არის ინტერვალი (2;3], რომელიც წარმოადგენს უტოლობათა სისტემის ამონახსნებს.

5. რაციონალური უტოლობების ამოხსნა ინტერვალის მეთოდით

ინტერვალების მეთოდი ემყარება ბინომის (x-a) შემდეგ თვისებას: x = α წერტილი ყოფს რიცხვთა ღერძს ორ ნაწილად - α წერტილიდან მარჯვნივ ბინომი (x-α)>0, ხოლო α წერტილიდან მარცხნივ (x-α)<0.

დაე, საჭირო იყოს უტოლობის ამოხსნა (x-α 1)(x-α 2)...(x-α n)>0, სადაც ფიქსირებულია α 1, α 2 ...α n-1, α n. რიცხვები, რომელთა შორის არ არის ტოლები და ისეთი, რომ α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 ინტერვალის მეთოდით მოქმედებენ შემდეგნაირად: რიცხვითი ღერძზე გამოსახულია α 1, α 2 ...α n-1, α n რიცხვები; მათგან ყველაზე დიდის მარჯვნივ, ე.ი. რიცხვები α n ჩადეთ პლუსის ნიშანი, მის შემდეგ შუალედში მარჯვნიდან მარცხნივ ჩადეთ მინუს ნიშანი, შემდეგ პლუს ნიშანი, შემდეგ მინუს ნიშანი და ა.შ. მაშინ უტოლობის ყველა ამონახსნის სიმრავლე (x-α 1)(x‑α 2)...(x-α n)>0 იქნება ყველა ინტერვალის გაერთიანება, რომელშიც მოთავსებულია პლუს ნიშანი და სიმრავლე უტოლობის ამონახსნები (x-α 1 )(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».

1) რაციონალური უტოლობების ამოხსნა (ანუ ფორმის უტოლობები P(x) Q(x) სადაც არის მრავალწევრები) ემყარება უწყვეტი ფუნქციის შემდეგ თვისებას: თუ უწყვეტი ფუნქცია ქრება x1 და x2 წერტილებში (x1; x2) და არ აქვს სხვა ფესვები ამ წერტილებს შორის, მაშინ ინტერვალებით (x1; x2) ფუნქცია ინარჩუნებს თავის ნიშანს.

მაშასადამე, რიცხვით წრფეზე y=f(x) ფუნქციის მუდმივი ნიშნის ინტერვალების საპოვნელად, მონიშნეთ ყველა ის წერტილი, რომლებზეც ფუნქცია f(x) ქრება ან განიცდის წყვეტას. ეს წერტილები რიცხვთა წრფეს ყოფენ რამდენიმე ინტერვალად, რომელთაგან თითოეულის შიგნით ფუნქცია f(x) უწყვეტია და არ ქრება, ე.ი. ინახავს ნიშანს. ამ ნიშნის დასადგენად საკმარისია ვიპოვოთ ფუნქციის ნიშანი რიცხვითი წრფის განხილული ინტერვალის ნებისმიერ წერტილში.

2) რაციონალური ფუნქციის მუდმივი ნიშნის ინტერვალების განსაზღვრა, ე.ი. რაციონალური უტოლობის ამოსახსნელად რიცხვთა წრფეზე აღვნიშნავთ მრიცხველის ფესვებს და მნიშვნელის ფესვებს, რომლებიც ასევე არის რაციონალური ფუნქციის ფესვები და წყვეტის წერტილები.

უტოლობების ამოხსნა ინტერვალის მეთოდით

3. < 20.

გამოსავალი. მისაღები მნიშვნელობების დიაპაზონი განისაზღვრება უტოლობების სისტემით:

f(x) = ფუნქციისთვის – 20. იპოვე f(x):

საიდანაც x = 29 და x = 13.

f(30) = – 20 = 0.3 > 0,

f(5) = – 1 – 20 = – 10< 0.

პასუხი:. რაციონალური განტოლებების ამოხსნის ძირითადი მეთოდები. 1) უმარტივესი: ამოხსნილია ჩვეულებრივი გამარტივებით - საერთო მნიშვნელამდე შემცირება, მსგავსი ტერმინების შემცირება და ა.შ. კვადრატული განტოლებები ax2 + bx + c = 0 ამოხსნილია...

X იცვლება ინტერვალზე (0,1] და მცირდება ინტერვალზე)